题目内容
有下列命题：
①G=
（G≠0）是a，G，b成等比数列的充分非必要条件；
②若角α，β满足cosαcosβ=1，则sin（α+β）=0；
③若不等式|x-4|+|x-3|＜a的解集非空，则必有a≥1；
④函数y=sinx+sin|x|的值域是[-2，2]．
其中正确命题的序号是
①G=
| ab |
②若角α，β满足cosαcosβ=1，则sin（α+β）=0；
③若不等式|x-4|+|x-3|＜a的解集非空，则必有a≥1；
④函数y=sinx+sin|x|的值域是[-2，2]．
其中正确命题的序号是
①②③④
①②③④
．（把你认为正确的命题的序号都填上）分析：根据等比数列的定义及性质，我们可以判断出①的真假；根据三角函数的值域，我们可以判断出②的真假；根据绝对值函数的值域，我们可以判断出③的真假，根据三角函数的值域，及分段函数的值域的求法，我们可判断④的真假，进而得到答案．
解答：解：当G=
（G≠0）时，a，b≠0，由等比数列的定义，可得a，G，b成等比数列，但a，G，b成等比数列时，G=±
，故①正确；
若角α，β满足cosαcosβ=1，则cosα=cosβ=1，或cosα=cosβ=-1，即α，β的终边同时落在x轴的正半轴上或负半轴上，则sin（α+β）=0，故②正确；
∵y=|x-4|+|x-3|≥1，故不等式|x-4|+|x-3|＜a的解集非空，则a≥1，故③正确；
当x≥0时，函数y=sinx+sin|x|=2sinx值域是[-2，2]；当x＜0时，函数y=sinx+sin|x|=0恒成立，故④正确；
故答案为：①②③④
| ab |
| ab |
若角α，β满足cosαcosβ=1，则cosα=cosβ=1，或cosα=cosβ=-1，即α，β的终边同时落在x轴的正半轴上或负半轴上，则sin（α+β）=0，故②正确；
∵y=|x-4|+|x-3|≥1，故不等式|x-4|+|x-3|＜a的解集非空，则a≥1，故③正确；
当x≥0时，函数y=sinx+sin|x|=2sinx值域是[-2，2]；当x＜0时，函数y=sinx+sin|x|=0恒成立，故④正确；
故答案为：①②③④
点评：本题考查的知识点是等比数列的定义及性质，三角函数的图象和性质，函数恒成立问题，其中利用上述基本知识点判断题目中四个命题的真假是解答本题的关键．
练习册系列答案
相关题目
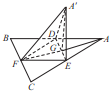如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列命题：
（G≠0）是a、G、b成等比数列的充分非必要条件；②若角α、β满足cosαcosβ=1，则sin（α+β）=0；③若不等式|x-4|+|x-3|＜a的解集非空，则必有a≥1；④函数y=sinx+sin|x|的值域是[-2，2].
（G≠0）是a、G、b成等比数列的充分非必要条件；②若角α、β满足cosαcosβ=1，则sin（α+β）=0；③若不等式|x-4|+|x-3|＜a的解集非空，则必有a≥1；④函数y=sinx+sin|x|的值域是[-2，2].