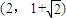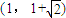题目内容
已知点F是椭圆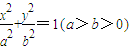 的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,PB⊥PA,则该椭圆的离心率e= .
的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,PB⊥PA,则该椭圆的离心率e= .
【答案】分析:由题意得该椭圆的形状确定,与大小无关.因此设a=1,得P(c,b2),从而A(-c,-b2),可得到直线AF的方程为:y=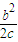 (x-c),与椭圆方程联解得出点B(
(x-c),与椭圆方程联解得出点B(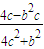 ,
,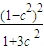 ),由此得出PB的斜率k1,并化简得k1=-2c,结合PA的斜率k2=
),由此得出PB的斜率k1,并化简得k1=-2c,结合PA的斜率k2=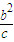 且PB⊥PA,由k1k2=-1列式并解之,可得b=c=
且PB⊥PA,由k1k2=-1列式并解之,可得b=c=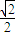 ,最终得出该椭圆的离心率e.
,最终得出该椭圆的离心率e.
解答:解: 根据题意椭圆的离心率为定值,故椭圆的形状确定,与大小无关
根据题意椭圆的离心率为定值,故椭圆的形状确定,与大小无关
因此设a=1,得椭圆的方程为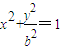 ,
,
求出椭圆的半焦距c,即得椭圆的离心率.
由F(c,0)及PF⊥x轴,得P(c,b2)
∵PA的中点为坐标原点O
∴A的坐标为(-c,-b2),得直线AF的斜率k=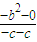 =
=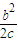
∴直线AF的方程为:y=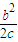 (x-c)
(x-c)
由 联解,得B的横坐标xB=
联解,得B的横坐标xB=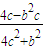 ,
,
将b2=1-c2代入,化简得xB=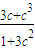 ,代入直线AF方程,得B的纵坐标yB=
,代入直线AF方程,得B的纵坐标yB=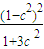
∴直线PB的斜率k1=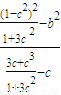 =-2c
=-2c
∵PA的斜率k2=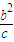 ,且PB⊥PA,
,且PB⊥PA,
∴k1k2=-1,得-2c•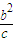 =-1,解之得b=c=
=-1,解之得b=c=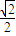
因此,该椭圆的离心率e=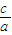 =
=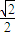
故答案为: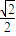
点评:本题给出满足特殊条件的椭圆,求该椭圆的离心率,着重考查了椭圆的标准方程和简单几何性质等知识,属于中档题.
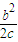 (x-c),与椭圆方程联解得出点B(
(x-c),与椭圆方程联解得出点B(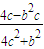 ,
,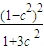 ),由此得出PB的斜率k1,并化简得k1=-2c,结合PA的斜率k2=
),由此得出PB的斜率k1,并化简得k1=-2c,结合PA的斜率k2=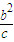 且PB⊥PA,由k1k2=-1列式并解之,可得b=c=
且PB⊥PA,由k1k2=-1列式并解之,可得b=c=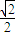 ,最终得出该椭圆的离心率e.
,最终得出该椭圆的离心率e.解答:解:
 根据题意椭圆的离心率为定值,故椭圆的形状确定,与大小无关
根据题意椭圆的离心率为定值,故椭圆的形状确定,与大小无关因此设a=1,得椭圆的方程为
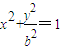 ,
,求出椭圆的半焦距c,即得椭圆的离心率.
由F(c,0)及PF⊥x轴,得P(c,b2)
∵PA的中点为坐标原点O
∴A的坐标为(-c,-b2),得直线AF的斜率k=
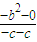 =
=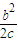
∴直线AF的方程为:y=
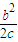 (x-c)
(x-c)由
 联解,得B的横坐标xB=
联解,得B的横坐标xB=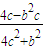 ,
,将b2=1-c2代入,化简得xB=
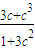 ,代入直线AF方程,得B的纵坐标yB=
,代入直线AF方程,得B的纵坐标yB=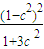
∴直线PB的斜率k1=
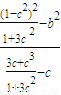 =-2c
=-2c∵PA的斜率k2=
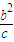 ,且PB⊥PA,
,且PB⊥PA,∴k1k2=-1,得-2c•
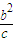 =-1,解之得b=c=
=-1,解之得b=c=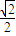
因此,该椭圆的离心率e=
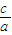 =
=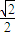
故答案为:
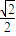
点评:本题给出满足特殊条件的椭圆,求该椭圆的离心率,着重考查了椭圆的标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
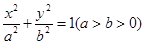 的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,
的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,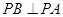 ,则该椭圆的离心率
,则该椭圆的离心率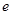 =___▲___.
=___▲___.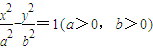 的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )