题目内容
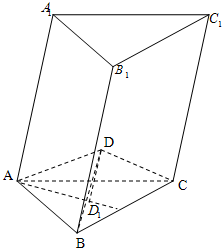 已知三棱锥D-ABC,D1为底面△ABC的重心,过A、B、C分别作DD1的平行线分别交对面所在的平面于A1,B1,C1点.(如,过A点作DD1的平行线交BCD所在的平面于A1点)
已知三棱锥D-ABC,D1为底面△ABC的重心,过A、B、C分别作DD1的平行线分别交对面所在的平面于A1,B1,C1点.(如,过A点作DD1的平行线交BCD所在的平面于A1点)(1)证明:AA1=3DD1;
(2)若DA、DB、DC两两垂直,且DA=DB=4,DC=3,求三棱锥D1-A1B1C1的体积.
分析:(1)根据A1是过A点作DD1的平行线与BCD所在的平面的交点,可得BC中点E与A1的连线必定经过点D,再在△AA1E中利用平行线分线段成比例定理,结合重心的性质,可证出AA1=3DD1;
(2)利用线面垂直的判定不难得到DC⊥平面ABD,可得VD-ABC=VC-ABD=8,结合(1)的结论可得三棱锥A1-ABC的体积是三棱锥D-ABC的三倍,得到VA1-ABC=24,最后根据等底等高的两个三棱锥的体积相等,可求出三棱锥D1-A1B1C1的体积.
(2)利用线面垂直的判定不难得到DC⊥平面ABD,可得VD-ABC=VC-ABD=8,结合(1)的结论可得三棱锥A1-ABC的体积是三棱锥D-ABC的三倍,得到VA1-ABC=24,最后根据等底等高的两个三棱锥的体积相等,可求出三棱锥D1-A1B1C1的体积.
解答: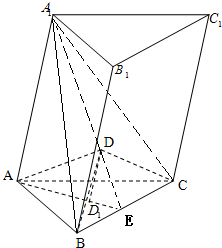 解:(1)∵点A1是过A点作DD1的平行线与BCD所在的平面的交点
解:(1)∵点A1是过A点作DD1的平行线与BCD所在的平面的交点
∴设BC中点为E,连接A1E,则点D必定在A1E上
∵△ABC中,D1为重心,∴AD1=3D1E
又∵△AA1E中,DD1∥AA1,
∴
=
=
,可得AA1=3DD1;
(2)连接A1B、A1C
∵DA⊥DB,DA=DB=4,∴S△ABD=
×4×4=8
∵DC⊥DB,DC⊥DA,且DA∩DB=D
∴DC⊥平面ABD,可得VD-ABC=VC-ABD=
×S△ABD×CD=8
∴VA1-ABC=3VD-ABC=24
∵三棱锥D1-A1B1C1与三棱锥A1-ABC等底等高
∴三棱锥D1-A1B1C1的体积V=24.
 解:(1)∵点A1是过A点作DD1的平行线与BCD所在的平面的交点
解:(1)∵点A1是过A点作DD1的平行线与BCD所在的平面的交点∴设BC中点为E,连接A1E,则点D必定在A1E上
∵△ABC中,D1为重心,∴AD1=3D1E
又∵△AA1E中,DD1∥AA1,
∴
| DD1 |
| AA1 |
| D1E |
| AE |
| 1 |
| 3 |
(2)连接A1B、A1C
∵DA⊥DB,DA=DB=4,∴S△ABD=
| 1 |
| 2 |
∵DC⊥DB,DC⊥DA,且DA∩DB=D
∴DC⊥平面ABD,可得VD-ABC=VC-ABD=
| 1 |
| 3 |
∴VA1-ABC=3VD-ABC=24
∵三棱锥D1-A1B1C1与三棱锥A1-ABC等底等高
∴三棱锥D1-A1B1C1的体积V=24.
点评:本题给出特殊的三棱柱,叫我们证明线段的倍数关系并且求三棱锥的体积,着重考查了线面垂直的判定、平行线的性质和锥体的体积公式等知识,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=
,BC=2,则二面角A-BC-D的大小是( )
| 3 |
| A、45° | B、60° |
| C、90° | D、120° |