Question

已知三棱锥D-ABC的三个侧面与底面全等，且AB=AC=

3

，BC=2，则以BC为棱，以面BCD与面BCA为面的二面角的余弦值为（　　）

• A．

  3

  3

• B．

  1

  3

• C．0
• D．-

  1

  2

Answer 1

分析：取BC中点E，连AE、DE，由题设知BC⊥AE，BC⊥DE，从而得到∠AED为二面角A-BC-D的平面角，由此能求出面BCD与面BCA为面的二面角的余弦值．

解答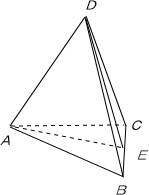：解：取BC中点E，连AE、DE，
∵三棱锥D-ABC的三个侧面与底面全等，且AB=AC=

3

，BC=2，
∴BC⊥AE，BC⊥DE，
∴∠AED为二面角A-BC-D的平面角
∵AB=AC=

3

，BC=2，
∴AE=ED=

2

，AD=2，∴∠AED=90°，
∴面BCD与面BCA为面的二面角的余弦值为0．
故选C．

点评：本题考查二面角的余弦值的求法，解题时要认真审题，仔细解答，注意空间想象能的培养．