题目内容
袋中装着分别标有数字1,2,3,4,5的5个形状相同的小球.
(1)从袋中任取2个小球,求两个小球所标数字之和为3的倍数的概率;
(2)从袋中有放回的取出2个小球,记第一次取出的小球所标数字为x,第二次为y,求点满足的概率.
(1)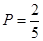 ;(2)
;(2)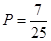 ;
;
解析试题分析:(1)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(3)注意判断是古典概型还是几何概型,基本事件前者是有限的,后者是无限的,两者都是等可能性.
试题解析:解 (1)任取2次,基本事件有:[1,2] [1,3] [1,4] [1,5] [2,3] [2,4] [2,5] [3,4] [3,5] [4,5],记“两数之和为3的倍数”为事件A,则事件A中含有:[1,2] [1,5] [2,4] [4,5]共4个基本事件,所以;
(2)有放回的取出2个,基本事件有:
(1,1)(1,2)(1,3)(1,4)(1,5)(2,1)(2,2)(2,3)(2,4)(2,5)
(3,1)(3,2)(3,3)(3,4)(3,5)(4,1)(4,2)(4,3)(4,4)(4,5)
(5,1)(5,2)(5,3)(5,4)(5,5)
记“点满足”为事件,则包含:(1,1)(1,2)(1,3)(2,1)(2,2)(3,1)(3,2)共7个基本事件 ,所以.
考点:利用古典概型求随机事件的概率.

练习册系列答案
相关题目
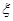 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求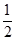 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: 的分别列与期望E
的分别列与期望E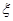 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求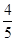 ,
,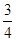 ,
,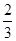 ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.