题目内容
下面四个命题：
①已知函数f(x)=
且f（a）+f（4）=4，那么a=-4；
②一组数据18，21，19，a，22的平均数是20，那么这组数据的方差是2；
③要得到函数y=sin(2x+
)的图象，只要将y=sin2x的图象向左平移
单位；
④已知奇函数f（x）在（0，+∞）为增函数，且f（-1）=0，则不等式f（x）＜0的解集{x|x＜-1}．
其中正确的是
①已知函数f(x)=
|
②一组数据18，21，19，a，22的平均数是20，那么这组数据的方差是2；
③要得到函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
④已知奇函数f（x）在（0，+∞）为增函数，且f（-1）=0，则不等式f（x）＜0的解集{x|x＜-1}．
其中正确的是
②
②
．分析：①因是分段函数，所以要讨论．②利用平均数和方差公式即可．③由横坐标的变换规律“左加右减”可得到变换后的表达式，再进行比较即可．④由已知条件画出图象即可得出答案．
解答：解：①∵f（4）=
=2，∴f（a）=4-f（4）=4-2=2．当a≥0时，f（a）=
=2，解得a=4；当a＜0时，f（a）=
=2，解得a=-4．故①不正确．
②∵（18+21+19+a+22）÷5=20，解得a=20，∴方差s2=
×[(-2)2+12+(-1)2+02+22]=2．故②正确．
③若将y=sin2x的图象向左平移
单位，得y=sin[2(x+
)]=sin(2x+
)=sin(π+2x-
)=-sin(2x-
)≠sin(2x+
)．故③不正确．
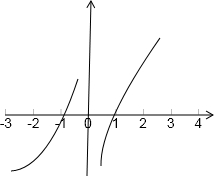
④由奇函数的图象关于原点对称，且函数f（x）在（0，+∞）为增函数，且f（-1）=0，可得f（1）=-f（-1）=0，（若f（x）在x=0有意义，则f（0）=0），如图所示：
∴不等式f（x）＜0的解集为{x|x＜-1，或0＜x＜1}．
故答案为②
| 4 |
| a |
| -a |
②∵（18+21+19+a+22）÷5=20，解得a=20，∴方差s2=
| 1 |
| 5 |
③若将y=sin2x的图象向左平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
④由奇函数的图象关于原点对称，且函数f（x）在（0，+∞）为增函数，且f（-1）=0，可得f（1）=-f（-1）=0，（若f（x）在x=0有意义，则f（0）=0），如图所示：
∴不等式f（x）＜0的解集为{x|x＜-1，或0＜x＜1}．
故答案为②
点评：本题综合考查了函数的性质、三角变换及统计量，深刻理解以上知识是解决问题的关键．
练习册系列答案
相关题目
，
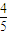,…的通项公式是an=
;③数列的图象是一群孤立的点；④数列1，-1，1，-1，…与数列-1，1，-1，1，…是同一个数列.其中正确命题的个数为…（ ）
，
，
，
，…的通项公式是an=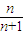
；