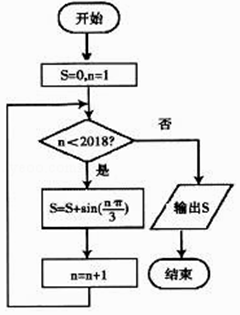
题目内容
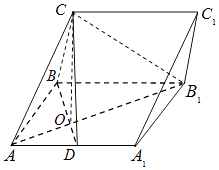
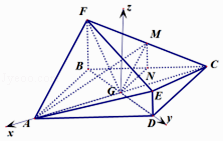
【题目】如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G. 
(I)求证:GM∥平面CDE;
(II)求直线AM与平面ACE成角的正弦值.
【答案】证明:(Ⅰ)取BC的中点N,连接GN,GM,MN.
因为G为菱形对角线的交点,所以G为AC中点,
又N为BC中点,所以GN∥CD,
又因为M,N分别为FC,BC的中点,
所以MN∥FB,又因为DE∥BF,
所以DE∥MN,
又MN∩GN=N,
所以平面GMN∥平面CDE,
又GM平面GMN,
所以GM∥平面CDE.
(Ⅱ)连接GF,设菱形的边长AB=2,则由∠ABC=120°,得 ![]() ,
,
又因为AF⊥FC,所以 ![]() ,
,
则在直角三角形GBF中, ![]() ,所以
,所以 ![]() ,
,
以G为坐标原点,分别以GA,GD所在直线为x轴,y轴,建立空间直角坐标系G﹣xyz,
则 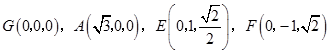 ,
, 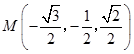
则 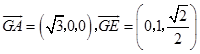 ,
,
设 ![]() 为平面ACE的一个法向量,则
为平面ACE的一个法向量,则 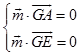 即
即 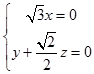 ,
,
令 ![]() ,得
,得 ![]() ,
,
又 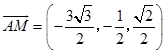 ,所以
,所以 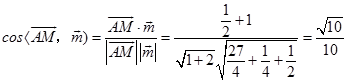 =
= 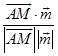 =
= 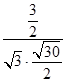 =
= ![]() ,
,
所以直线AM与平面ACE所成角的正弦值为 ![]() .
.
【解析】(I)取BC的中点N,连接GN,GM,MN.由MN∥BF∥DE,GN∥CD可得平面GMN∥平面CDE,故而GM∥平面CDE;(II)以G为原点,建立空间坐标系,求出平面ACE的法向量 ![]() 和
和 ![]() 的坐标,计算
的坐标,计算 ![]() 和
和 ![]() 的夹角即可得出结论.
的夹角即可得出结论.
【考点精析】通过灵活运用直线与平面平行的判定和空间角的异面直线所成的角,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则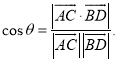 即可以解答此题.
即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目