Question

若过椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的焦点且垂直于x轴的直线被椭圆截得的线段长为

1

2

a，则该椭圆的离心率是（　　）

• A、

  3

  2

• B、

  3

  4

• C、

  1

  4

• D、

  1

  2

Answer 1

分析：首先根据题意，设椭圆的焦点坐标为A、B，CD为椭圆上的过点B且与x轴垂直的弦，可得CB=

a

4

；由椭圆的定义，可得CA=

7a

4

；在Rt△CAD中，由勾股定理可得，AB=

3

a；结合椭圆的定义可得，2c=

3

a，即可得答案．

解答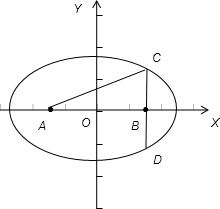：解：设椭圆的焦点坐标为A、B，CD为椭圆上的过点B且与x轴垂直的弦，
根据题意，有CD=

1

2

a，则CB=

1

2

CD=

a

4

；
由椭圆的定义，可得CA=

7a

4

；
由勾股定理可得，AB=

3

a；
而椭圆的焦点坐标为A、B，即AB=2c；
则2c=

3

a，
可得e=

c

a

=

3

2

；
故选A．

点评：本题考查椭圆的定义，注意结合题意，灵活应用椭圆的有关性质的使用．