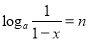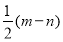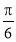题目内容
已知直线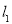 过点
过点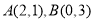 ,直线
,直线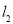 的斜率为
的斜率为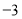 且过点
且过点 .
.
(1)求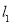 、
、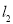 的交点
的交点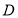 的坐标;
的坐标;
(2)已知点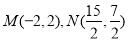 ,若直线
,若直线 过点
过点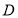 且与线段
且与线段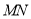 相交,求直线
相交,求直线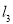 的斜率
的斜率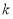 的取值范围.
的取值范围.
(1)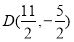 ;(2)
;(2)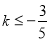 或
或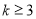 .
.
【解析】
试题分析:(1)先由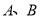 两点的坐标求出斜率
两点的坐标求出斜率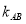 ,然后由直线的点斜式写出直线
,然后由直线的点斜式写出直线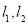 的方程,最后联立方程求解即可得到交点
的方程,最后联立方程求解即可得到交点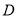 的坐标;(2)法一:先由点斜式写出直线
的坐标;(2)法一:先由点斜式写出直线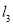 的方程
的方程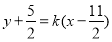 ,由
,由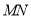 两点的坐标写出线段
两点的坐标写出线段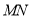 的方程
的方程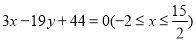 ,联立这两个方程,求出交点的横坐标
,联立这两个方程,求出交点的横坐标 ,然后求解不等式
,然后求解不等式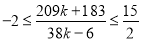 即可得到
即可得到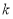 的取值范围;法二:采用数形结合,先分别求出边界直线
的取值范围;法二:采用数形结合,先分别求出边界直线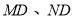 的斜率,由图分析就可得到
的斜率,由图分析就可得到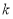 的取值范围.
的取值范围.
试题解析:(1)∵直线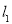 过点
过点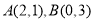
∴直线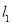 的方程为
的方程为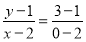 ,即
,即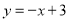 2分
2分
又∵直线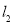 的斜率为
的斜率为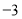 且过点
且过点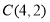
∴直线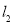 的方程为
的方程为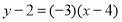 ,即
,即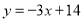 4分
4分
∴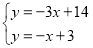 ,解得
,解得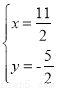 即
即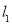 、
、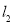 的交点
的交点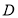 坐标为
坐标为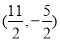 6分
6分
说明:在求直线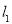 的方程的方程时还可以利用点斜式方程或一般式方程形式求解
的方程的方程时还可以利用点斜式方程或一般式方程形式求解
(2)法一:由题设直线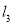 的方程为
的方程为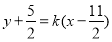 7分
7分
又由已知可得线段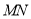 的方程为
的方程为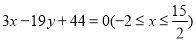 8分
8分
∵直线 且与线段
且与线段 相交
相交
∴
解得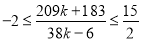 10分
10分
得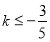 或
或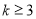
∴直线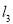 的斜率
的斜率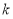 的取值范围为
的取值范围为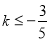 或
或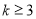 12分
12分
法二:由题得下图, 7分

∵ 8分
8分
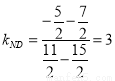 9分
9分
∴直线 的斜率
的斜率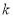 的取值范围为
的取值范围为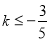 或
或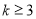 12分.
12分.
考点:1.由两点求直线的斜率;2.直线的方程;3.两直线的交点问题.

练习册系列答案
相关题目