题目内容
矩形ABCD的边长分别为a、b,P是CD的中点,把矩形ABCD沿AP、BP折成一个三棱锥的三个侧面,求这三个侧面中面积最大的侧面与底面所成的二面角的正弦值.

答案:
解析:
解析:
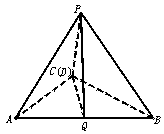
解:由原图可知△PAB的面积最大. 在如图三棱锥P—ABC中,
∵PC⊥BC,PD⊥DA, ∴PC(D)⊥面ABC(D). ∴作PQ⊥AB于Q,连结CD, ∴CQ⊥AB. ∴∠PQC为侧面PAB与底面ACB所成的二面角的平面角. ∵PA=PB,PQ⊥AB, ∴PQ为AB边上的中线, ∴PQ=b, ∵PC=
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
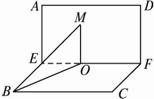
 (2008•杭州二模)正方形ABCD的边长是2,E,F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图所示).M为矩形AEFD内一点,如果∠MBE=∠MBC,MB和平面BCF所成角的正切值为
(2008•杭州二模)正方形ABCD的边长是2,E,F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图所示).M为矩形AEFD内一点,如果∠MBE=∠MBC,MB和平面BCF所成角的正切值为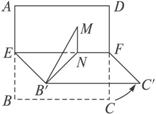
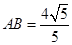 ,一块直角三角板
,一块直角三角板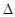 PBD的边
PBD的边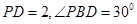 ,且
,且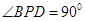 ,如图.
,如图.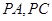 的长;
的长;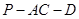 的平面角的余弦值.
的平面角的余弦值.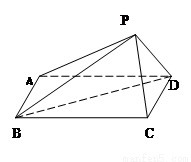
 ,一块三角板
,一块三角板 PBD的边
PBD的边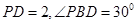 ,且
,且 ,如图.
,如图.
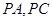 的长;
的长; 的体积
的体积