题目内容
选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤.A、选修4-1:
几何证明选讲.如图,圆O的直径AB=4,C为圆周上一点,BC=2,过C作圆O的切线l,过A作l的垂线AD,AD分别与直线l、圆O交于点D,E,求∠DAC的度数与线段AE的长.
B、选修4-2:矩阵变换
求圆C:x2+y2=4在矩阵A=[
 ]的变换作用下的曲线方程.
]的变换作用下的曲线方程.C、选修4-4:坐标系与参数方程
若两条曲线的极坐标方程分别为ρ=1与ρ=2sinθ,它们相交于A、B两点,求线段AB的长.
D、选修4-5:不等式选讲
已知a、b、c为正数,且满足acos2θ+bsin2θ<c.求证:
 cos2θ+
cos2θ+ sin2θ<
sin2θ< .
.
【答案】分析:A:先利用弦切角定理求得∠DCA=60°,从而解直角三角形得∠DAC的度数,最后证明△AOE为等边三角形从而求得线段AE的长;B:设P(x,y)是圆C:x2+y2=4上的任意一点,P′(x′,y′)是P(x,y)在矩阵A=[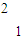 ]的对应变换作用下新曲线上的对应点,则由矩阵的运算性质得点P和点P′坐标间的关系,代入P点轨迹即可得所求曲线方程;C:先将已知曲线方程联立,得交点的极坐标,在利用极坐标的定义,在三角形中通过解三角形求得AB的长;D:由柯西不等式定理直接证明即可
]的对应变换作用下新曲线上的对应点,则由矩阵的运算性质得点P和点P′坐标间的关系,代入P点轨迹即可得所求曲线方程;C:先将已知曲线方程联立,得交点的极坐标,在利用极坐标的定义,在三角形中通过解三角形求得AB的长;D:由柯西不等式定理直接证明即可
解答:解;A:如图,在Rt△ABC中,AB=2BC,∴∠ABC=60°,
由于l为过C的切线,∠DCA=∠CBA,∴∠DCA=60°,
又∵AD⊥DC,得∠DAC=30°.
那么在△AOE中,∠EAO=∠DAC+∠CAB=60°,OE=OA,
∴AE=AO= AB=2
AB=2
B:设P(x,y)是圆C:x2+y2=4上的任意一点,
设P′(x′,y′)是P(x,y)在矩阵A=[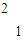 ]的对应变换作用下新曲线上的对应点,
]的对应变换作用下新曲线上的对应点,
则[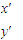 ]=[
]=[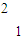 ][
][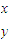 ]=[
]=[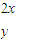 ],
],
即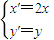 ,代入x2+y2=4得
,代入x2+y2=4得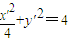
∴曲线方程为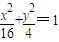
C:解:由ρ=1与ρ=2sinθ,得2sinθ=1
θ=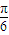 或θ=
或θ=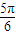
∴A、B的极坐标为A(1,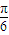 ),(1,
),(1,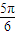 )
)
在△AOB中,OA=OB=1,∠AOB=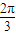
∴AB=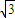
D:证明:由柯西不等式可得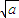 cos2θ+
cos2θ+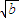 sin2θ≤[(
sin2θ≤[(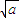 cosθ)2+(
cosθ)2+(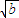 sinθ)2]0.5(cos2θ+sin2θ)0.5
sinθ)2]0.5(cos2θ+sin2θ)0.5
=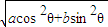 <
<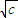
点评:本题综合考查了平面几何证明,直线与圆的性质定理,矩阵变换和矩阵运算,极坐标系及其与直角坐标系的互化,利用柯西不等式证明不等式的方法
 ]的对应变换作用下新曲线上的对应点,则由矩阵的运算性质得点P和点P′坐标间的关系,代入P点轨迹即可得所求曲线方程;C:先将已知曲线方程联立,得交点的极坐标,在利用极坐标的定义,在三角形中通过解三角形求得AB的长;D:由柯西不等式定理直接证明即可
]的对应变换作用下新曲线上的对应点,则由矩阵的运算性质得点P和点P′坐标间的关系,代入P点轨迹即可得所求曲线方程;C:先将已知曲线方程联立,得交点的极坐标,在利用极坐标的定义,在三角形中通过解三角形求得AB的长;D:由柯西不等式定理直接证明即可解答:解;A:如图,在Rt△ABC中,AB=2BC,∴∠ABC=60°,
由于l为过C的切线,∠DCA=∠CBA,∴∠DCA=60°,
又∵AD⊥DC,得∠DAC=30°.
那么在△AOE中,∠EAO=∠DAC+∠CAB=60°,OE=OA,
∴AE=AO=
 AB=2
AB=2B:设P(x,y)是圆C:x2+y2=4上的任意一点,
设P′(x′,y′)是P(x,y)在矩阵A=[
 ]的对应变换作用下新曲线上的对应点,
]的对应变换作用下新曲线上的对应点,则[
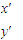 ]=[
]=[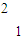 ][
][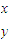 ]=[
]=[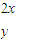 ],
],即
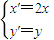 ,代入x2+y2=4得
,代入x2+y2=4得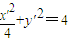
∴曲线方程为
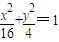
C:解:由ρ=1与ρ=2sinθ,得2sinθ=1
θ=
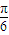 或θ=
或θ=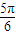
∴A、B的极坐标为A(1,
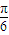 ),(1,
),(1,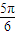 )
)在△AOB中,OA=OB=1,∠AOB=
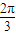
∴AB=
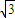
D:证明:由柯西不等式可得
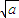 cos2θ+
cos2θ+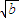 sin2θ≤[(
sin2θ≤[(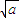 cosθ)2+(
cosθ)2+(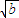 sinθ)2]0.5(cos2θ+sin2θ)0.5
sinθ)2]0.5(cos2θ+sin2θ)0.5=
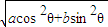 <
<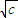
点评:本题综合考查了平面几何证明,直线与圆的性质定理,矩阵变换和矩阵运算,极坐标系及其与直角坐标系的互化,利用柯西不等式证明不等式的方法

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤.
(2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤. A.(选修4—1:几何证明选讲)
A.(选修4—1:几何证明选讲)