题目内容
已知两个正数a,b满足a+b=ab,则a+b的最小值为
- A.1
- B.2
- C.4
- D.2

C
分析:由基本不等式可得a+b=ab≤ =
=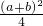 ,化为关于(a+b)的不等式,解之即可.
,化为关于(a+b)的不等式,解之即可.
解答:由题意可得a+b=ab≤ =
=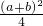
化简可得(a+b)2-4(a+b)≥0,
解得a+b≥4,或a+b≤0(ab为正数,故舍去)
故a+b的最小值为4
故选C
点评:本题考查基本不等式求最值,涉及一元二次不等式的解法,属基础题.
分析:由基本不等式可得a+b=ab≤
 =
=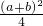 ,化为关于(a+b)的不等式,解之即可.
,化为关于(a+b)的不等式,解之即可.解答:由题意可得a+b=ab≤
 =
=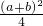
化简可得(a+b)2-4(a+b)≥0,
解得a+b≥4,或a+b≤0(ab为正数,故舍去)
故a+b的最小值为4
故选C
点评:本题考查基本不等式求最值,涉及一元二次不等式的解法,属基础题.

练习册系列答案
相关题目
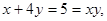 则xy最小值x,y值分别是 ( )
则xy最小值x,y值分别是 ( )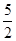 C.10,5 D.10,10
C.10,5 D.10,10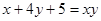 ,则xy取最小值时x,y的值分别是 (
)
,则xy取最小值时x,y的值分别是 (
)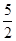 C.10,5 D.10,10
C.10,5 D.10,10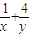 的最小值”,给出如下一种解法:
的最小值”,给出如下一种解法: =
=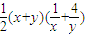 =
=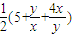 ,
,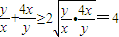 ,∴
,∴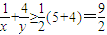 ,
,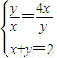 ,即
,即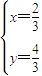 时,
时,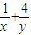 取最小值
取最小值 .
.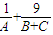 的最小值为 .
的最小值为 .