题目内容
给出函数封闭的定义:若对于定义域D内的任一个自变量x0,都有函数值f(x0)∈D,则称函数y=f(x)在D上封闭.
(1)若定义域D1=(0,1),判断下列函数中哪些在D1上封闭,且给出推理过程f1(x)=2x-1,f2(x)=-
x2-
x+1,f3(x)=2x-1,f4(x)=cosx.;
(2)若定义域D2=(1,2),是否存在实数a使函数f(x)=
在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.
(1)若定义域D1=(0,1),判断下列函数中哪些在D1上封闭,且给出推理过程f1(x)=2x-1,f2(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)若定义域D2=(1,2),是否存在实数a使函数f(x)=
| 5x-a |
| x+2 |
(1)∵f1(
)=0∉(0,1),
∴f(x)在D1上不封闭;
∵f2(x)=-(x+
)2+
在(0,1)上是减函数,
∴0<f2(1)<f2(x)<f2(0)=1,
∴f2(x)∈(0,1)?f2(x)在D1上封闭;
∵f3(x)=2x-1在(0,1)上是增函数,∴0=f3(0)<f3(x)<f3(1)=1,
∴f3(x)∈(0,1)?f3(x)在D1上封闭;
∵f4(x)=cosx在(0,1)上是减函数,∴cos1=f4(1)<f4(x)<f4(0)=1,
∴f4(x)∈(cos1,1)?(0,1)?f4(x)在D1上封闭;
(2)f(x)=5-
,假设f(x)在D2上封闭,对a+10讨论如下:
若a+10>0,则f(x)在(1,2)上为增函数,故应有
?
?a=2
若a+10=0,则f(x)=5,此与f(x)∈(1,2)不合,
若a+10<0,则f(x)在(1,2)上为减函数,故应有
?
,无解,
综上可得,a=2时f(x)在D2上封闭.
| 1 |
| 2 |
∴f(x)在D1上不封闭;
∵f2(x)=-(x+
| 1 |
| 2 |
| 9 |
| 8 |
∴0<f2(1)<f2(x)<f2(0)=1,
∴f2(x)∈(0,1)?f2(x)在D1上封闭;
∵f3(x)=2x-1在(0,1)上是增函数,∴0=f3(0)<f3(x)<f3(1)=1,
∴f3(x)∈(0,1)?f3(x)在D1上封闭;
∵f4(x)=cosx在(0,1)上是减函数,∴cos1=f4(1)<f4(x)<f4(0)=1,
∴f4(x)∈(cos1,1)?(0,1)?f4(x)在D1上封闭;
(2)f(x)=5-
| a+10 |
| x+2 |
若a+10>0,则f(x)在(1,2)上为增函数,故应有
|
|
若a+10=0,则f(x)=5,此与f(x)∈(1,2)不合,
若a+10<0,则f(x)在(1,2)上为减函数,故应有
|
|
综上可得,a=2时f(x)在D2上封闭.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,都有函数值
,都有函数值 ,则称函数y=f(x)在 D上封闭。
,则称函数y=f(x)在 D上封闭。 判断下列函数中哪些在
判断下列函数中哪些在 上封闭,并给出推理过程;
上封闭,并给出推理过程;
 是否存在实数
是否存在实数 ,使函数
,使函数 在
在 上封闭,若存在,求出
上封闭,若存在,求出 -
- +1,f3(x)=2x-1;
+1,f3(x)=2x-1;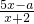 在D2上封闭?若存在,求出a的值,并给出证明;若不存在,请说明理由.
在D2上封闭?若存在,求出a的值,并给出证明;若不存在,请说明理由.