题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,满足(c-2a)cosB+bcosC=0
(1)求角B的大小;


(2)若a=2,cosA=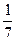 ,求c的值
,求c的值
(1)求角B的大小;



(2)若a=2,cosA=
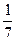 ,求c的值
,求c的值B="60º" ,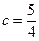
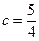
解:(1)△ABC中,由正弦定理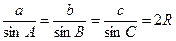 有
有


a=2RsinA,b=2RsinB,c=2RsinC.
代入整理可得 (sinC-2sinA)cosB+sinBcosC=0,…………………………2分
即 sinCcosB+sinBcosC=2sinAcosB,
∴ sin(B+C)=2sinAcosB,…………………………………………………4分
由A+B+C=π知B+C=π-A,
∴ sin(π-A)=2sinAcosB,
即 sinA=2sinAcosB,
由sinA≠0得cosB=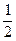 .
.
∴B=60º.…………………………………………………………………6分
(2)∵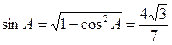 ,
,
∴ sinC=sin(A+B)=sinAcosB+cosAsinB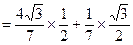
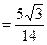 .
.
由正弦定理有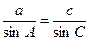 即
即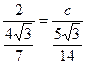 ,解得
,解得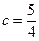 .……………10分
.……………10分
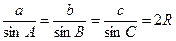 有
有


a=2RsinA,b=2RsinB,c=2RsinC.
代入整理可得 (sinC-2sinA)cosB+sinBcosC=0,…………………………2分
即 sinCcosB+sinBcosC=2sinAcosB,
∴ sin(B+C)=2sinAcosB,…………………………………………………4分
由A+B+C=π知B+C=π-A,
∴ sin(π-A)=2sinAcosB,
即 sinA=2sinAcosB,
由sinA≠0得cosB=
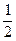 .
.∴B=60º.…………………………………………………………………6分
(2)∵
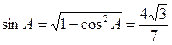 ,
,∴ sinC=sin(A+B)=sinAcosB+cosAsinB
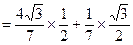
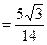 .
.由正弦定理有
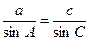 即
即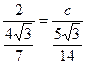 ,解得
,解得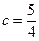 .……………10分
.……………10分
练习册系列答案
相关题目
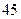 分钟,我海军舰艇在
分钟,我海军舰艇在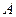 处获悉后,立即测出该渔船在方位角为
处获悉后,立即测出该渔船在方位角为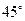 距离为
距离为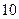 海里的
海里的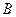 处,并测得渔船以
处,并测得渔船以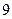 海里/时的速度正沿方位角为
海里/时的速度正沿方位角为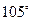 的方向漂移,我军舰艇立即以
的方向漂移,我军舰艇立即以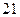 海里/时的速度前往营救.求出我军舰艇赶上遇险渔船所需的最短时间,问能否营救成功?
海里/时的速度前往营救.求出我军舰艇赶上遇险渔船所需的最短时间,问能否营救成功?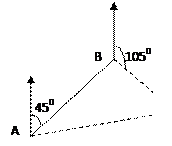
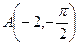 ,
,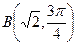 ,
,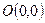 ,则
,则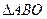 为( )
为( )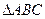 中,若
中,若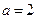 ,则
,则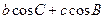 等于
等于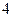
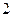
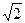
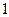
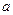 ,
,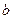 ,
,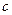 ,若∠C=120°,
,若∠C=120°,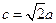 ,则
,则 ★ .
★ .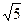 ,b=
,b=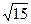 ,A=30°,则c= .
,A=30°,则c= .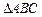 中,角
中,角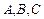 的对边分别为
的对边分别为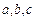 ,已知
,已知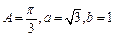 ,则
,则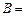
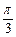
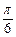
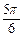
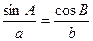 ,则B的值为( )
,则B的值为( ) 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3 +3
+3 -3
-3 =4
=4 bc .
bc . 的值.
的值.