题目内容
已知椭圆 ,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为
,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为 ,且
,且
(I)求此椭圆的方程;
(II)设直线A1P和直线BQ的倾斜角分别为α、β,试判断α+β是否为定值?若是,求出此定值;若不是,请说明理由.

【答案】分析:(I)根据椭圆的离心率求得a和c的关系,利用勾股定理求得a和b的关系式,最后联立求得a和b,则椭圆的方程可得.
(II)由(I)可值A2(2,0),B(0,1),利用l∥A2B,求得直线l的斜率,设出直线l的方程,与椭圆的方程联立,消去y,利用韦达定理表示出x1+x2和x1+x2,然后分别表示出tanα和tanβ,令二者相加,化简整理求得结果为0,进而可利用正切的两角和公式求得tan(α+β)=0,判断出α+β=π是定值.
解答:解:(I)由已知可得
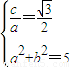 ,求得a=2,b=1
,求得a=2,b=1
∴椭圆方程为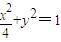
(II)α+β是定值π.
由(I)A2(2,0),B(0,1),且l∥A2B,所以直线l的斜率k=- ,
,
设直线l的方程为y=- x+m,P(x1,y1),Q(x2,y2),
x+m,P(x1,y1),Q(x2,y2),
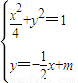 ,x2-2mx+2m2-2=0
,x2-2mx+2m2-2=0
∴△=4m2-4(2m2-2)=8-4m2≥0,即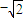 ≤m≤
≤m≤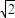
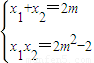
∵P、Q两点不是椭圆的顶点∴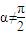 、
、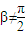
∴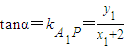 ,
,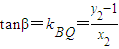
又因为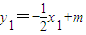 ,
,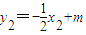
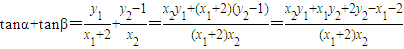
=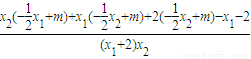
=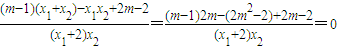
∴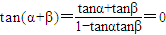 ,又α,β∈(0,π)
,又α,β∈(0,π)
∴α+β∈(0,2π)∴α+β=π是定值
点评:本题主要考查了直线与圆锥曲线的综合问题.考查运用解析几何的方法分析问题和解决问题的能力.
(II)由(I)可值A2(2,0),B(0,1),利用l∥A2B,求得直线l的斜率,设出直线l的方程,与椭圆的方程联立,消去y,利用韦达定理表示出x1+x2和x1+x2,然后分别表示出tanα和tanβ,令二者相加,化简整理求得结果为0,进而可利用正切的两角和公式求得tan(α+β)=0,判断出α+β=π是定值.
解答:解:(I)由已知可得
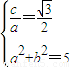 ,求得a=2,b=1
,求得a=2,b=1∴椭圆方程为
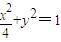
(II)α+β是定值π.
由(I)A2(2,0),B(0,1),且l∥A2B,所以直线l的斜率k=-
 ,
,设直线l的方程为y=-
 x+m,P(x1,y1),Q(x2,y2),
x+m,P(x1,y1),Q(x2,y2),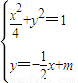 ,x2-2mx+2m2-2=0
,x2-2mx+2m2-2=0∴△=4m2-4(2m2-2)=8-4m2≥0,即
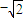 ≤m≤
≤m≤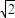
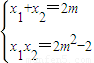
∵P、Q两点不是椭圆的顶点∴
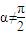 、
、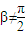
∴
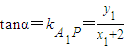 ,
,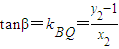
又因为
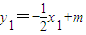 ,
,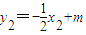
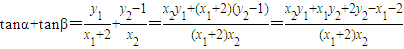
=
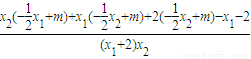
=
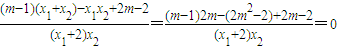
∴
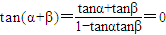 ,又α,β∈(0,π)
,又α,β∈(0,π)∴α+β∈(0,2π)∴α+β=π是定值
点评:本题主要考查了直线与圆锥曲线的综合问题.考查运用解析几何的方法分析问题和解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为
,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为 ,且
,且
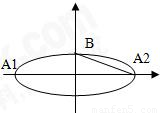
 ,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为
,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为 ,且
,且

 ,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为
,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为 ,且
,且

 ,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为
,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为 ,且
,且
