题目内容
设椭圆的中心是坐标原点,长轴在x轴上,离心率e= ,已知点P(0,
,已知点P(0, )到椭圆上的点的最远距离是
)到椭圆上的点的最远距离是 ,求这个椭圆方程。
,求这个椭圆方程。
【答案】
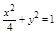
【解析】主要考查椭圆的几何性质及椭圆方程的求法。利用待定系数法。
解: ∵e2==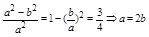
∴椭圆方程可设为: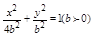
设A(x,y)是椭圆上任一点,则:│PA│2=x2+(y-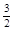 )2=-3y2-3y+4b2+
)2=-3y2-3y+4b2+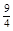
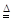 f(y)(-b≤y≤b)
f(y)(-b≤y≤b)
讨论:1°、-b>-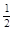
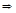 0<b<
0<b<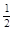 时,│PA│
时,│PA│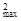 = f(-b)=(b+
= f(-b)=(b+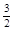 )2
)2
=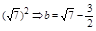 ,但b>
,但b>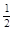 ,矛盾。不合条件。
,矛盾。不合条件。
2°、-b≤-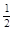
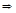 b≥
b≥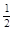 时,│PA│
时,│PA│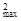 = f(-
= f(-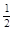 )=4b2+3=7
)=4b2+3=7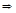 b2=1
b2=1
∴所求椭圆为: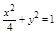

练习册系列答案
相关题目