题目内容
过P(2,1)作直线L与x轴正半轴、y轴的正半轴分别交于A、B两点,设∠BAO=2α(O为坐标原点),当△AOB的周长最小时,cotα=
3
3
.分析:先用2α的三角函数表示△AOB的周长,进而导数求最值,从而得解.
解答:解:由题意,△AOB的周长可表示为OA+OB+PA+PB=2+cot2α+1+2tan2α+
+
令tan2α=t,则周长为y=3+
+2t+
+ 2
y/=-
+2-
+
令y′=0,可得t=
∵函数在区间(0,
)上单调减,在(
,+∞)上单调增,
∴函数在t=
时,取得极小值,且为最小值.
∴当tan2α=
时,周长最小
∴
=
∴tanα=
∴cotα=3
故答案为:3
| 1 |
| sin2α |
| 2 |
| cos2α |
令tan2α=t,则周长为y=3+
| 1 |
| t |
| ||
| t |
| t2+1 |
y/=-
| 1 |
| t2 |
| 1 | ||
t2
|
| 2t | ||
|
令y′=0,可得t=
| 3 |
| 4 |
∵函数在区间(0,
| 3 |
| 4 |
| 3 |
| 4 |
∴函数在t=
| 3 |
| 4 |
∴当tan2α=
| 3 |
| 4 |
∴
| 2 tanα |
| 1-tan2α |
| 3 |
| 4 |
∴tanα=
| 1 |
| 3 |
∴cotα=3
故答案为:3
点评:本题以直线为载体,考查导数的运用,计算要细心.

练习册系列答案
相关题目
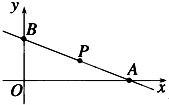 过点P(2,1)作直线l分别交x,y正半轴于A,B两点.
过点P(2,1)作直线l分别交x,y正半轴于A,B两点.