题目内容
平面上有一个△ABC和一点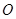 ,设
,设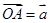 ,
,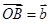 ,
,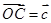 ,又
,又 、
、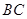 的中点分别为
的中点分别为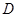 、
、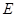 ,则向量
,则向量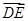 等于( )
等于( )
A.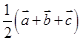 | B.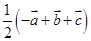 |
C.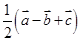 | D.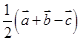 |
B
解析试题分析:根据题意可知E为BC的中点,D为OA的中点,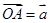 ,
,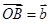 ,
,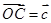 ,由中点公式,可知
,由中点公式,可知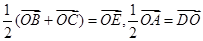
所以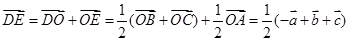 ,选B.
,选B.
考点:本试题主要考查了向量中点公式的应用,以及两个向量的加减法的法则和几何意义。
点评:解决该试题的关键是利用E为BC的中点,D为OA的中点,得到,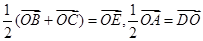

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
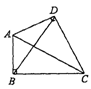
如图,在四边形ABCD中,AB⊥BC,AD⊥DC,.若 则
则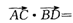 ( )
( )
| A.a2-b2 | B.b2-a2 | C.a2+b2 | D.ab |
已知向量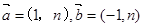 ,若
,若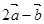 与
与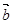 垂直,则
垂直,则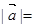 ( )
( )
A.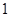 | B.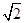 | C.4 | D.2 |
已知平面向量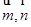 的夹角为
的夹角为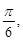 且
且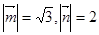 ,在
,在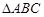 中,
中,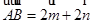 ,
,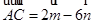 ,
,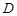 为
为 中点,则
中点,则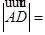 ( )
( )
| A.2 | B.4 | C.6 | D.8 |
已知向量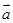 、
、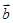 不共线,
不共线, ,如果
,如果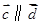 ,那么
,那么
A.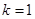 且 且 与 与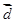 同向 同向 | B.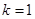 且 且 与 与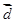 反向 反向 |
C.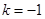 且 且 与 与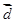 同向 同向 | D.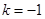 且 且 与 与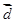 反向 反向 |
向量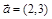 在向量
在向量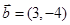 上的正射影的数量为 ( )
上的正射影的数量为 ( )
A.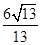 | B.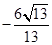 | C.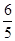 | D.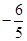 |
已知向量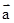 ,
,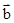 满足
满足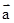 ·
·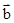 =0,│
=0,│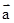 │=1,│
│=1,│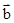 │=2,则│2
│=2,则│2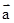 -
-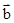 │=( )
│=( )
| A.0 | B.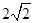 | C. 4 | D.8 |
若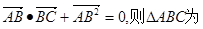 ( )
( )
| A.直角三角形 | B.钝角三角形 |
| C.锐角三角形 | D.等腰三角形 |
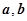 满足
满足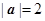 ,
,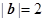 ,
,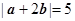 ,则向量
,则向量