题目内容
10.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1).分析 构造函数g(x)=$\frac{f(x)}{x}$,利用g(x)的导数判断函数g(x)的单调性与奇偶性,
画出函数g(x)的大致图象,结合图形求出不等式f(x)>0的解集.
解答  解:设g(x)=$\frac{f(x)}{x}$,则g(x)的导数为:
解:设g(x)=$\frac{f(x)}{x}$,则g(x)的导数为:
g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵当x>0时总有xf′(x)<f(x)成立,
即当x>0时,g′(x)恒小于0,
∴当x>0时,函数g(x)=$\frac{f(x)}{x}$为减函数,
又∵g(-x)=$\frac{f(-x)}{-x}$=$\frac{-f(x)}{-x}$=$\frac{f(x)}{x}$=g(x),
∴函数g(x)为定义域上的偶函数
又∵g(-1)=$\frac{f(-1)}{-1}$=0,
∴函数g(x)的大致图象如图所示:
数形结合可得,不等式f(x)>0?x•g(x)>0
?$\left\{\begin{array}{l}{x>0}\\{g(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{g(x)<0}\end{array}\right.$,
?0<x<1或x<-1.
∴f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1).
故答案为:(-∞,-1)∪(0,1).
点评 本题考查了利用导数判断函数的单调性,并由函数的奇偶性和单调性解不等式的应用问题,是综合题目.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
18.下列对应不是从集合A到集合B的映射是( )
| A. | A={直角坐标平面上的点},B={(x,y)|x∈R,y∈R},对应法则是:A中的点与B中的(x,y)对应 | |
| B. | A={平面内的圆},B={平面内的三角形},对应法则是:作圆的内接三角形 | |
| C. | A=N,B={0,1},对应法则是:除以2的余数 | |
| D. | A={0,1,2},B={4,1,0},对应法则是f:x→y=x2. |
2.已知向量$\overrightarrow a$=(1,2),$\overrightarrow b$=(m,1),如果向量$\overrightarrow a$与$\overrightarrow b$平行,则m的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
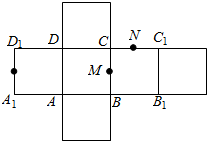 如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,
如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,