题目内容
(12分)已知函数f(X)=㏒a(ax-1) (a>0且a≠1 )
)
(1)求函数的定义域 (2)讨论函数f(X)的单调性
 )
)(1)求函数的定义域 (2)讨论函数f(X)的单调性
解:(1) ax-1>0 , ax>1=a0 当a>1时,X>0 当0<a<1时,X<0
所以当a>1时,f(X)定义域是(0,+∞)
当0<a<1时,f(X)定义域是(-∞,0)
(2)当a>1时,Y=㏒au是增函数,U=ax-1 是增函数,所以f(X)=㏒a(a x-1)在(0,+∞)上是增函数。
同理可证当0<a<1时 函数f(X)在(-∞,0)上也是增函数。
所以当a>1时,f(X)定义域是(0,+∞)
当0<a<1时,f(X)定义域是(-∞,0)
(2)当a>1时,Y=㏒au是增函数,U=ax-1 是增函数,所以f(X)=㏒a(a x-1)在(0,+∞)上是增函数。
同理可证当0<a<1时 函数f(X)在(-∞,0)上也是增函数。
略

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
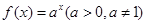 ,
,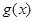 为
为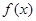 的反函数.若
的反函数.若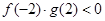 ,那么
,那么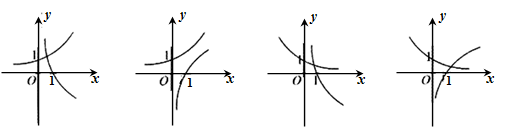
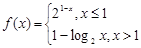 ,则满足
,则满足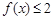 的
的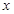 的取值范围是 ( )
的取值范围是 ( )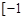 ,2]
,2]
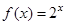 ,
,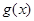 是一次函数,并且点
是一次函数,并且点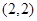 在函数
在函数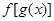 的图象上,点
的图象上,点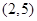 在函数
在函数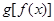 的图象上,求
的图象上,求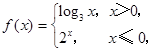 则
则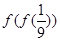 的值为 .
的值为 . 不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象成为衰变,假设在放射性同位素铯1
不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象成为衰变,假设在放射性同位素铯1 量
量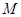 (单位:太贝克)与时间
(单位:太贝克)与时间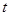 (单位:年)满足函数关系:
(单位:年)满足函数关系: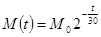
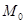 为
为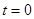 时铯137的含量,已知
时铯137的含量,已知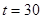 时,铯137的含量的变化率是
时,铯137的含量的变化率是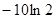 (太贝克/年),则
(太贝克/年),则 太贝克.
太贝克.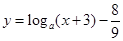 (
(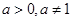 )的图像恒过定点A,若点A也在函数
)的图像恒过定点A,若点A也在函数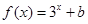 的图像上,则
的图像上,则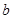 =
= 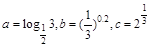 ,则
,则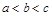
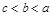
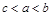
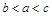
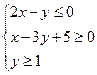 ,则
,则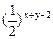 的最大值是_________
的最大值是_________