题目内容
定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线的l距离.则曲线C:x2+(y+4)2=2到直线l:y=x的距离为
.
| 2 |
| 2 |
分析:由题意得曲线C表示以M(0,-4)为圆心、半径r=
的圆.设A为曲线C上的动点,AB是点A到直线l的垂线段,可得当线段AB与点M到l的垂线段重合时,AB长可达最小值.由此利用点到直线的距离公式加以计算,可得答案.
| 2 |
解答:解: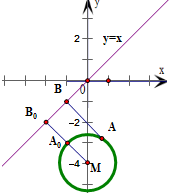 ∵曲线C方程为x2+(y+4)2=2,
∵曲线C方程为x2+(y+4)2=2,
∴曲线C表示以M(0,-4)为圆心、半径r=
的圆.
设A为曲线C上的动点,作AB⊥直线l于点B,
可得当线段AB与点M到l的垂线段重合时,AB长可达最小值.
∵M到直线l的距离为d=
=2
,
∴曲线C到直线的l距离为d-r=
.
故答案为:
.
 ∵曲线C方程为x2+(y+4)2=2,
∵曲线C方程为x2+(y+4)2=2,∴曲线C表示以M(0,-4)为圆心、半径r=
| 2 |
设A为曲线C上的动点,作AB⊥直线l于点B,
可得当线段AB与点M到l的垂线段重合时,AB长可达最小值.
∵M到直线l的距离为d=
| |0+4| | ||
|
| 2 |
∴曲线C到直线的l距离为d-r=
| 2 |
故答案为:
| 2 |
点评:本题给出曲线到直线的距离的定义,求圆到定直线的距离.着重考查了圆的标准方程、点到直线的距离公式等知识,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目