题目内容
点M到点F(2,0)的距离比它到直线x=-3的距离小1.
①求M的轨迹方程;
②若过F(2,0)点倾斜角为45°的直线与M的轨迹交于A、B两点,求△ABO面积.
①求M的轨迹方程;
②若过F(2,0)点倾斜角为45°的直线与M的轨迹交于A、B两点,求△ABO面积.
分析:①由题意得点M到点F(2,0)的距离等于M到直线x=-2的距离,根据抛物线定义,可得点M的轨迹是以F为焦点、直线x=-2为准线的抛物线,求出抛物线的方程为y2=8x,即可得到点M的轨迹方程;
②算出直线AB的方程为y=x-2,与抛物线方程联解,消去y可得y2-8y-16=0.设A(x1,y1)、B(x2,y2),利用一元二次方程根与系数的关系算出|y1-y2|=8
,再根据三角形面积公式加以计算,可得△AB0的面积.
②算出直线AB的方程为y=x-2,与抛物线方程联解,消去y可得y2-8y-16=0.设A(x1,y1)、B(x2,y2),利用一元二次方程根与系数的关系算出|y1-y2|=8
| 2 |
解答:解:①设M(x,y),
∵点M到点F(2,0)的距离比它到直线x=-3的距离小1,
∴点M到点F(2,0)的距离等于M到直线x=-2的距离
由抛物线定义得:点M的轨迹是以F为焦点、直线x=-2为准线的抛物线.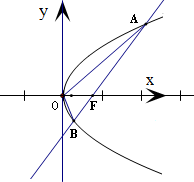
设抛物线方程为y2=2px(p>0),可得
=2,p=4,
∴抛物线的方程为y2=8x,即为点M的轨迹方程;
②∵直线的倾斜角为45°,
∴直线的斜率k=tan45°=1,
可得直线的方程为y=1×(x-2),即y=x-2.
由
消去x,整理得y2-8y-16=0.
设A(x1,y1)、B(x2,y2),则y1+y2=8,y1y2=-16,
∴|y1-y2|=
=
=8
,
因此,△AB0的面积S=
|OF|•|y1-y2|=
×2×8
=8
.
∵点M到点F(2,0)的距离比它到直线x=-3的距离小1,
∴点M到点F(2,0)的距离等于M到直线x=-2的距离
由抛物线定义得:点M的轨迹是以F为焦点、直线x=-2为准线的抛物线.

设抛物线方程为y2=2px(p>0),可得
| p |
| 2 |
∴抛物线的方程为y2=8x,即为点M的轨迹方程;
②∵直线的倾斜角为45°,
∴直线的斜率k=tan45°=1,
可得直线的方程为y=1×(x-2),即y=x-2.
由
|
设A(x1,y1)、B(x2,y2),则y1+y2=8,y1y2=-16,
∴|y1-y2|=
| (y1+y2)2-4y 1y2 |
| 64-4×(-16) |
| 2 |
因此,△AB0的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题求动点M的轨迹方程,并依此求满足条件的△AB0的面积.着重考查了抛物线的定义与标准方程、一元二次方程根与系数的关系、直线与圆锥曲线的位置关系等知识,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目