题目内容
定义函数 ,若存在常数
,若存在常数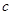 ,对任意
,对任意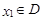 ,存在唯一
,存在唯一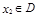 的,使得
的,使得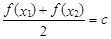 ,则称函数
,则称函数 在
在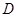 上的均值为
上的均值为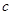 ,已知
,已知 ,则函数
,则函数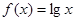 在
在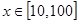 上的均值为。( )
上的均值为。( )
A.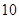 | B. | C.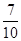 | D. |
D
解析试题分析:根据定义,函数 ,若存在常数
,若存在常数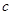 ,对任意的
,对任意的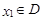 ,存在唯一的
,存在唯一的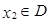 ,使得
,使得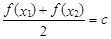 ,则称函数
,则称函数 在
在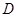 上的均值为
上的均值为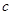 ,令
,令 ,当
,当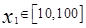 时,选定
时,选定 可得:
可得: ,故选D.
,故选D.
考点:平均值不等式.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
一次函数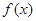 的图象过点
的图象过点 和
和 ,则下列各点在函数
,则下列各点在函数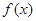 的图象上的是( )
的图象上的是( )
A. | B. | C. | D. |
已知 是函数
是函数 的一个零点,若
的一个零点,若 ,则( )
,则( )
A. | B. |
C. | D. |
已知函数 有
有 个零点,则实数
个零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.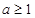 | D. |
若函数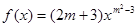 是幂函数,则
是幂函数,则 的值为( )
的值为( )
A.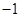 | B. | C.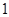 | D.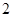 |
已知函数 若关于
若关于 的方程
的方程 有三个不等的实根,则实数
有三个不等的实根,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若 ,则
,则 的取值范围是__________.
的取值范围是__________.
A.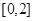 | B. | C. | D. |
在下列区间中,函数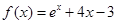 的零点所在的区间为( )
的零点所在的区间为( )
A.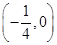 | B.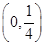 | C.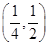 | D.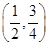 |
函数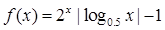 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |