题目内容
是定义在
上的偶函数且在
上递增,不等式
的解集为
【答案】
【解析】
试题分析：利用函数的奇偶性可把不等式转化到区间[0，+∞）上，再由单调性可去掉不等式中的符号“f”，从而化为具体不等式解决。解：因为f（x）为R上的偶函数，所以
等价于
，因为又f（x）在[0，+∞）上递增，所以
,故答案为
考点：函数奇偶性、单调性
点评：本题考查函数奇偶性、单调性的综合应用及抽象不等式的求解，解决本题的关键是利用函数性质化抽象不等式为具体不等式处理
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
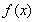
是定义在
上的偶函数,且当
时,
的解集为 （ ）
B．
D．随a的值而变化
上的偶函数, 且在( 0 , + 
)上是减函数，如果
，且
，则有（ ）
B.
D.
是定义在
上的偶函数,且在
上单调递增,则不等式
的解集是( )
B．
C．
∪
D．不能确定