题目内容
已知
、
是同一平面内两个不共线的向量，
=
+k
，
=2
-
，若
与
是共线向量，则实数k的值等于
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
-
| 1 |
| 2 |
-
．| 1 |
| 2 |
分析：利用向量共线定理和平面向量基本定理即可得出．
解答：解：∵
与
是共线向量，∴?实数λ，使得
=λ
，
∴
+k
=λ(2
-
)，化为(1-2λ)
+(k+λ)
=
．
∵
、
是同一平面内两个不共线的向量，
∴
，解得
．
故答案为-
．
| a |
| b |
| a |
| b |
∴
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| 0 |
∵
| e1 |
| e2 |
∴
|
|
故答案为-
| 1 |
| 2 |
点评：熟练掌握向量共线定理和平面向量基本定理是解题的关键．
练习册系列答案
相关题目
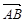=e1+e2，
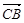=－λe1－8e2,
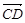=3e1－3e2,若A、B、D三点在同一条直线上，求实数λ的值.
=e1+e2，
=-λe1-8e2，
=3e1-3e2，若A、B、D三点在同一条直线上，求实数λ的值．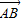
=e1+e2，
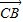=-λe1-8e2，
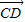=3e1-3e2，若A、B、D三点在同一条直线上，求实数λ的值．