题目内容

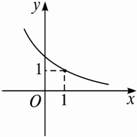
定义在R上的函数y=f(x-1)是单调递减函数(如图所示),给出四个结论,其中正确结论的个数是(   )

①f(0)=1 ②f(1)<1 ③f -1(1)=0     ④f -1()>0

  A.1                B.2                C.3                D.4

D

解析:由图知,当x=1时,f(x-1)=1,即f(0)=1.

∴①正确.

∵y=f(x)的反函数存在,

∴f-1(1)=0.

∴③正确.

由题意知x=2时,f(x-1) ＜<1,即f(1)＜1.

∴②正确.

∵y=f(x-1)单调递减,

∴y=f -1(x)单调递减.

由图知, ＜f(0),

∴f -1()＞f -1［f(0)］=0.

∴④正确.

练习册系列答案
相关题目
11、定义在R上的函数y=f（x）满足f（-x）=-f（x），f（1+x）=f（1-x），当x∈[-1，1]时，f（x）=x3，则f（2009）的值是（　　）
13、定义在R上的函数y=f（x）满足：f（x）=f（4-x），且f（x-2）+f（2-x）=0，则f（508）=
0
．
定义在R上的函数y=f(x)满足f(3-x)=f(x)，(x-
3
2
)f′(x)＞0(x≠
3
2
)，若x1＜x2，且x1+x2＞3，则有（　　）
下列四个命题：
①“a＞b”是“2a＞2b”成立的充要条件；
②“a=b”是“lga=lgb”成立的充分不必要条件；
③函数f（x）=ax2+bx（x∈R）为奇函数的充要条件是“a=0”
④定义在R上的函数y=f（x）是偶函数的必要条件是“
f(-x)f(x)
=1”．
其中真命题的序号是
①③
①③
．（把真命题的序号都填上）
定义在R上的函数y=f（x）满足f（-x）=-f（x），f（1+x）=f（1-x），当x∈[-1，1]时，f（x）=x3，则f（2011）=
-1
-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网