题目内容
正四面体的四个面上分别写有数字0,1,2,3,把两个这样的四面体抛在桌面上,则露在外面的6个数字恰好是2,0,1,3,0,3的概率为 .
【答案】分析:由题意可知:两个四面体有一个1朝下,另一个2朝下,且那个面朝下是独立的,分别可得概率为 ,由概率的乘法的公式可得答案.
,由概率的乘法的公式可得答案.
解答:解:由题意可知:两个四面体有一个1朝下,另一个2朝下,
可知每个四面体1朝下的概率为 ,2朝下的概率也为
,2朝下的概率也为 ,
,
故所求事件的概率为:P=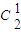 ×
×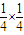 =
=
故答案为:
点评:本题考查古典概型及概率的计算公式,涉及独立事件的概率,属基础题.
 ,由概率的乘法的公式可得答案.
,由概率的乘法的公式可得答案.解答:解:由题意可知:两个四面体有一个1朝下,另一个2朝下,
可知每个四面体1朝下的概率为
 ,2朝下的概率也为
,2朝下的概率也为 ,
,故所求事件的概率为:P=
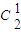 ×
×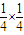 =
=
故答案为:

点评:本题考查古典概型及概率的计算公式,涉及独立事件的概率,属基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目