题目内容
设双曲线的中心在原点,准线平行于x轴,离心率为
剖析:由双曲线中心在原点,准线平行于x轴,可设双曲线的方程为![]() -
-![]() =1.
=1.
由离心率为![]() ,可得a2+b2=(
,可得a2+b2=(![]() a)2=c2.
a)2=c2.
由点P(0,5)到此双曲线上的点的最近距离为2,可转化为二次函数的最大(小)值问题来讨论,得到a、b应满足的另一关系式.从而求出a2、b2,本题得解.
解:依题意,设双曲线的方程为![]() -
-![]() =1(a>0,b>0).
=1(a>0,b>0).
∵e=![]() =
=![]() ,c2=a2+b2,
,c2=a2+b2,
∴a2=4b2.
设M(x,y)为双曲线上任一点,则
|PM|2=x2+(y-5)2
=b2(![]() -1)+(y-5)2
-1)+(y-5)2
=![]() (y-4)2+5-b2(|y|≥2b).
(y-4)2+5-b2(|y|≥2b).
①若4≥2b,则当y=4时,
|PM|min2=5-b2=4,得b2=1,a2=4.
从而所求双曲线方程为![]() -x2=1.
-x2=1.
②若4<2b,则当y=2b时,
|PM|min2=4b2-20b+25=4,
得b=![]() (舍去b=
(舍去b=![]() ),b2=
),b2=![]() ,a2=49.
,a2=49.
从而所求双曲线方程为![]() -
-![]() =1.
=1.

练习册系列答案
相关题目
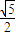 ,且点P(0,5)到此双曲线上的点的最近距离为2,求双曲线的方程.
,且点P(0,5)到此双曲线上的点的最近距离为2,求双曲线的方程.