题目内容

下列命题中：
①若
a
•
b
=0，则
a
=
0
或
b
=
0
；  
②若不平行的两个非零向量
a
，
b
满足 |
a
|=|
b
|，则(
a
+
b
)•(
a
-
b
)=0；   
③若
a
与
b
平行，则|
a
•
b
|=|
a
|•|
b
|； 
④若
a
∥
b
，
b
∥
c
则
a
∥
c
；
其中真命题的个数是（　　）
分析：根据向量垂直的充要条件，可判断①；根据向量模的定义及向量的数量积运算法则，可判断②，根据向量数量积的定义，可判断③；根据零向量的特殊性，可判断④
解答：解：若
a
•
b
=0，则
a
=
0
或
b
=
0
或
a
⊥
b
，故①错误．
两个向量
a
，
b
满足 |
a
|=|
b
|，则(
a
+
b
)•(
a
-
b
)=
a
2-
b
2=|
a
|2-|
b
|2=0，故②正确．
若
a
与
b
同向，则|
a
•
b
|=|
a
|•|
b
|；若
a
与
b
反向，则|
a
•
b
|=-|
a
|•|
b
|，故③错误；
当
b
=
0
，由零向量与任意向量平行，可知
a
∥
c
不一定成立，故④错误；
故真命题的个数是1个
故选A
点评：本题以命题的真假判断为载体考查了向量数量积的定义，向量垂直的充要条件等知识点，难度不大，属于基础题．
练习册系列答案
相关题目
下列命题中正确的是(    )

A．x2≠y2x≠y或x≠-y

B．命题“若a、b都是偶数，则a+b是偶数”的逆否命题是“若a+b不是偶数，则a、b都不是偶数”

C．若“p或q”为假则“非p且非q”为真

D．“|x|＜2”是“x2-x-6＜0”的必要非充分条件

下列命题中正确的是(  )

A．命题“若,则”的否命题为“若,则”

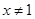B．“”是“”的必要不充分条件

C．命题“,使得”的否定是“,均有”

D．命题“在中,若,则”的逆否命题为真命题

 

设m、n是两条不同的直线，、β是两个不同的平面，则下列命题中正确的是

A．若m∥n，m∥，则n∥

B．若⊥β，m∥，则m⊥β

C．若⊥β，m⊥β，则m∥

D．若m⊥n，m⊥，n⊥β，则⊥β

 

已知m，n是两条不同直线，α、β、γ是三个不同平面．下列命题中正确的是

A．若m∥α，n∥α，则m∥n      B．若α⊥γ，β⊥γ，则α∥β

C．若m∥α，m∥β，则α∥β      D．若m⊥α，n⊥α，则m∥n

 

若函数唯一的一个零点同时在区间（0，16），（0，8），（0，4），（0，2）内，那么下列命题中正确的是(      ).

    A. 函数在区间（0，1）内有零点   B. 函数在区间（0，1）或（1，2）内有零点

    C. 函数在区间（2，16）内无零点  D. 函数在区间（1，16）内无零点

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网