题目内容
若非空集合S={1、2、3、4、5}且若a∈S，则必有6-a∈S，则所有满足上述条件的集合S共有（ ）
分析：通过a∈S，则必有6-a∈S，有1必有5，有2必有4，然后利用列举法列出所求可能即可．
解答：解：由题意知，集合S中包含的元素可以是3，1和5，2和4中的一组、两组、三组，
即S={3}，{1，5}，{2，4}，{3，1，5}，{3，2，4}，{1，5，2，4}，{3，1，5，2，4}，
故选B．
即S={3}，{1，5}，{2，4}，{3，1，5}，{3，2，4}，{1，5，2，4}，{3，1，5，2，4}，
故选B．
点评：本题主要考查了子集的定义，以及集合的限制条件下求满足条件的集合，属于基础题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
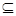{1,2,3,4,5}，且若a∈S，则必有6－a∈S，则所有满足上述条件的集合S共有（ ）