题目内容
(本题满分12分)
已知数列 的前
的前 项和为
项和为 ,
, (
( ).
).
(Ⅰ)证明数列 是等比数列,求出数列
是等比数列,求出数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅲ)数列 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
【答案】
(Ⅰ)见解析,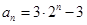 .
.
(Ⅱ)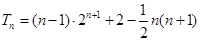 .
.
(Ⅲ)不存在满足条件的三项.
【解析】本题主要考查了数列的递推式的应用,数列的通项公式和数列的求和问题.应熟练掌握一些常用的数列的求和方法如公式法,错位相减法,叠加法等.
(1)把Sn和Sn+1相减整理求得an+1=2an+3,整理出3+an+1=2(3+an),判断出数列{3+an}是首相为6,公比为2的等比数列,求得3+an,则an的表达式可得.
(2)把(I)中的an代入bn,求得其通项公式,进而利用错位相减法求得数列的前n项的和.
(3)设存在满足题意,那么等式两边的奇数和偶数来分析不存在。
解析:(Ⅰ)因为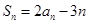 ,所以
,所以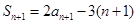 ,
,
则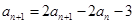 ,所以
,所以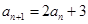 ,
,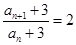 ,
,
所以数列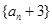 是等比数列,
是等比数列,
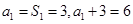 ,
,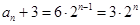 ,
,
所以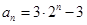 .
.
(Ⅱ)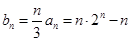 ,
,
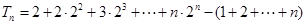 ,
,
令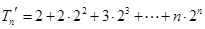 ,①
,①
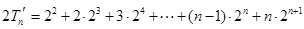 ,②
,②
①-②得,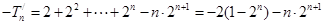 ,
,
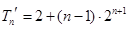 ,
,
所以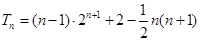 .
.
(Ⅲ)设存在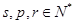 ,且
,且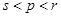 ,使得
,使得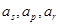 成等差数列,
成等差数列,
则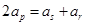 ,
,
即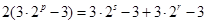 ,
,
即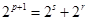 ,
,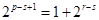 ,因为
,因为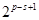 为偶数,
为偶数,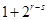 为奇数,
为奇数,
所以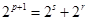 不成立,故不存在满足条件的三项.
不成立,故不存在满足条件的三项.

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面