题目内容
已知:在函数f(x)=mx3-x的图象上,以N(1,n)为切点的切线的倾斜角为 .
.(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式f(x)≤k-1993对于x∈[-1,3]恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
(3)求证:
 (x∈R,t>0).
(x∈R,t>0).
【答案】分析:(1)由函数f(x)=mx3-x,可求出f'(x)的解析式,根据以N(1,n)为切点的切线的倾斜角为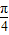 ,构造方程可以求出m的值,进而求出n值,
,构造方程可以求出m的值,进而求出n值,
(2)由(1)中结论,我们可以求出函数的解析式,由于f(x)≤k-1993对于x∈[-1,3]恒成立,我们可以求出x∈[-1,3]的最大值,进而确定满足条件的k值;
(3)方法一:根据(1)中函数的解析式,根据三角函数的值域和基本不等式,我们分别求出|f(sinx)+f(cosx)|的最大值和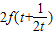 的最小值,比照后即可得到答案.
的最小值,比照后即可得到答案.
方法二:根据(2)的结论,我们可以确定出函数的单调性,结合绝对值的性质和基本不等式,利用函数的单调性可以结论.
解答:解:(1)f'(x)=3mx2-1,依题意,得f'(1)= ,即3m-1=1,
,即3m-1=1,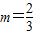 .…(2分)
.…(2分)
∵f(1)=n,∴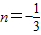 .…(3分)
.…(3分)
(2)令f'(x)=2x2-1=0,得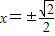 .…(4分)
.…(4分)
当 时,f'(x)=2x2-1>0;
时,f'(x)=2x2-1>0;
当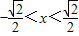 时,f'(x)=2x2-1<0;
时,f'(x)=2x2-1<0;
当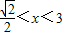 时,f'(x)=2x2-1>0.
时,f'(x)=2x2-1>0.
又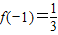 ,
,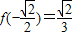 ,
,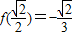 ,f(3)=15.
,f(3)=15.
因此,当x∈[-1,3]时,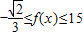 .…(7分)
.…(7分)
要使得不等式f(x)≤k-1993对于x∈[-1,3]恒成立,则k≥15+1993=2008.
所以,存在最小的正整数k=2008,使得不等式f(x)≤k-1993对于x∈[-1,3]恒成立.…(9分)
(3)方法一:|f(sinx)+f(cosx)|=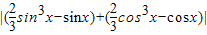 =
=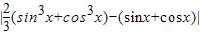 =
=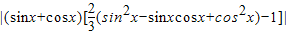 =
=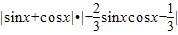 =
= =
=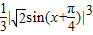
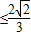 .…(11分)
.…(11分)
又∵t>0,∴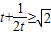 ,
,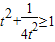 .
.
∴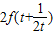 =
=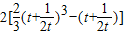 =
=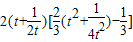
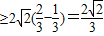 .…(13分)
.…(13分)
综上可得,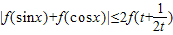 (x∈R,t>0).…(14分)
(x∈R,t>0).…(14分)
方法二:由(2)知,函数f(x)在[-1,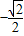 ]上是增函数;在[
]上是增函数;在[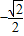 ,
,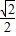 ]上是减函数;在[
]上是减函数;在[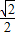 ,1]上是增函数.
,1]上是增函数.
又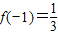 ,
,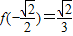 ,
, ,
,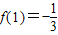 .
.
所以,当x∈[-1,1]时,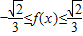 ,即
,即 .
.
∵sinx,cosx∈[-1,1],∴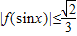 ,
,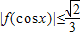 .
.
∴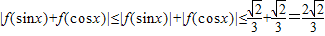 .…(11分)
.…(11分)
又∵t>0,∴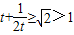 ,且函数f(x)在[1,+∞)上是增函数.
,且函数f(x)在[1,+∞)上是增函数.
∴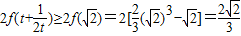 .…(13分)
.…(13分)
综上可得,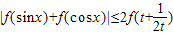 (x∈R,t>0).…(14分)
(x∈R,t>0).…(14分)
点评:本题考查的知识点是不等式的证明,导数的几何意义,利用导数研究函数的单调性,直线的倾斜角,其中根据已知条件,求出函数的解析式,并分析出函数的性质是解答本题的关键.
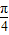 ,构造方程可以求出m的值,进而求出n值,
,构造方程可以求出m的值,进而求出n值,(2)由(1)中结论,我们可以求出函数的解析式,由于f(x)≤k-1993对于x∈[-1,3]恒成立,我们可以求出x∈[-1,3]的最大值,进而确定满足条件的k值;
(3)方法一:根据(1)中函数的解析式,根据三角函数的值域和基本不等式,我们分别求出|f(sinx)+f(cosx)|的最大值和
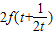 的最小值,比照后即可得到答案.
的最小值,比照后即可得到答案.方法二:根据(2)的结论,我们可以确定出函数的单调性,结合绝对值的性质和基本不等式,利用函数的单调性可以结论.
解答:解:(1)f'(x)=3mx2-1,依题意,得f'(1)=
 ,即3m-1=1,
,即3m-1=1,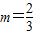 .…(2分)
.…(2分)∵f(1)=n,∴
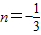 .…(3分)
.…(3分)(2)令f'(x)=2x2-1=0,得
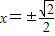 .…(4分)
.…(4分)当
 时,f'(x)=2x2-1>0;
时,f'(x)=2x2-1>0;当
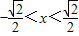 时,f'(x)=2x2-1<0;
时,f'(x)=2x2-1<0;当
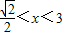 时,f'(x)=2x2-1>0.
时,f'(x)=2x2-1>0.又
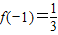 ,
,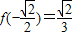 ,
,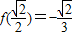 ,f(3)=15.
,f(3)=15.因此,当x∈[-1,3]时,
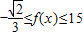 .…(7分)
.…(7分)要使得不等式f(x)≤k-1993对于x∈[-1,3]恒成立,则k≥15+1993=2008.
所以,存在最小的正整数k=2008,使得不等式f(x)≤k-1993对于x∈[-1,3]恒成立.…(9分)
(3)方法一:|f(sinx)+f(cosx)|=
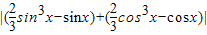 =
=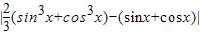 =
=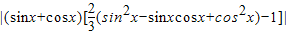 =
=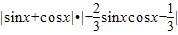 =
= =
=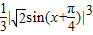
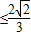 .…(11分)
.…(11分)又∵t>0,∴
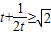 ,
,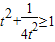 .
.∴
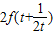 =
=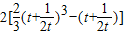 =
=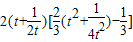
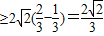 .…(13分)
.…(13分)综上可得,
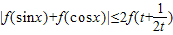 (x∈R,t>0).…(14分)
(x∈R,t>0).…(14分)方法二:由(2)知,函数f(x)在[-1,
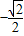 ]上是增函数;在[
]上是增函数;在[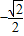 ,
,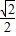 ]上是减函数;在[
]上是减函数;在[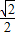 ,1]上是增函数.
,1]上是增函数.又
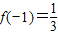 ,
,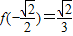 ,
, ,
,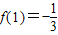 .
.所以,当x∈[-1,1]时,
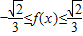 ,即
,即 .
.∵sinx,cosx∈[-1,1],∴
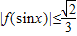 ,
,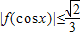 .
.∴
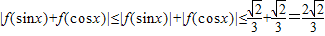 .…(11分)
.…(11分)又∵t>0,∴
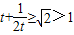 ,且函数f(x)在[1,+∞)上是增函数.
,且函数f(x)在[1,+∞)上是增函数.∴
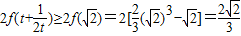 .…(13分)
.…(13分)综上可得,
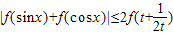 (x∈R,t>0).…(14分)
(x∈R,t>0).…(14分)点评:本题考查的知识点是不等式的证明,导数的几何意义,利用导数研究函数的单调性,直线的倾斜角,其中根据已知条件,求出函数的解析式,并分析出函数的性质是解答本题的关键.

练习册系列答案
相关题目
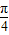 .
.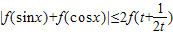 (x∈R,t>0).
(x∈R,t>0).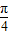 .
.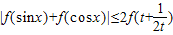 (x∈R,t>0).
(x∈R,t>0).