题目内容
设sinα+cosα=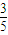 ,则sin2α= .
,则sin2α= .
【答案】分析:将已知的等式两边平方,利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,即可求出sin2α的值.
解答:解:把sinα+cosα=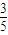 两边平方得:
两边平方得:
(sinα+cosα)2=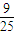 ,
,
即sin2α+cos2α+2sinαcosα=1+sin2α=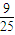 ,
,
解得:sin2α=-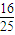 .
.
故答案为:-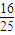
点评:此题考查了同角三角函数间的基本关系,以及二倍角的正弦函数公式.将已知的等式两边平方是本题的突破点.
解答:解:把sinα+cosα=
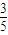 两边平方得:
两边平方得:(sinα+cosα)2=
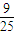 ,
,即sin2α+cos2α+2sinαcosα=1+sin2α=
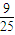 ,
,解得:sin2α=-
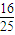 .
.故答案为:-
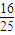
点评:此题考查了同角三角函数间的基本关系,以及二倍角的正弦函数公式.将已知的等式两边平方是本题的突破点.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是
 上一点.设∠TAP=θ,长方形PQCR的面积为S平方米.
上一点.设∠TAP=θ,长方形PQCR的面积为S平方米.