题目内容
设曲线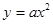 在点(1,
在点(1,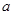 )处的切线与直线
)处的切线与直线 平行,则
平行,则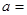 ( )
( )
| A.1 | B.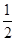 | C.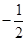 | D.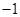 |
A
解析试题分析:利用曲线在切点处的导数为斜率求曲线的切线斜率,利用直线平行它们的斜率相等列方程,从而可求切线方程.解:求导函数y'=2ax,∴x=1时,y'=2a,∵曲线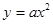 (a≠0)在(1,a)处的切线与直线2x-y-6=0平行,∴有2a=2,∴a=1,故可知选A.
(a≠0)在(1,a)处的切线与直线2x-y-6=0平行,∴有2a=2,∴a=1,故可知选A.
考点:导数的几何意义
点评:本题考查两条直线平行,考查导数的几何意义:曲线在切点处的导数值是切线的斜率.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
函数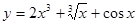 ,则导数
,则导数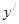 =( )
=( )
A.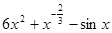 | B. |
C.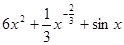 | D. |
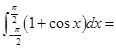 ( )
( )
A. | B.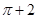 | C.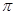 | D.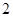 |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
| A.-1<a<2 | B.-3<a<6 | C.a<-1或a>2 | D.a<-3或a>6 |
将和式的极限 表示成定积分( )
表示成定积分( )
A.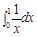 | B. | C. | D. |
函数 的导数是( )
的导数是( )
A. | B. | C. | D. |
满足 的函数是
的函数是
| A.f(x)=1-x | B.f(x)=x |
| C.f(x)=0 | D.f(x)=1 |
若 ,则k=
,则k=
| A.1 | B.0 | C.0或1 | D.以上都不对 |
一物体在力 (
( 单位为
单位为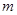 ,
, 单位为
单位为 )的作用下,沿着与力
)的作用下,沿着与力 相同的方向从
相同的方向从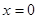 处运动到
处运动到 处,则力
处,则力 所作的功是:
所作的功是:
| A.40 | B.42 | C.48 | D.52 |