题目内容

f（x）=（m-1）x2+2mx+3是偶函数，则f（-1），f(-
2
)，f(
3
)的大小关系为（　　）
A、f(-
2
)＜f(
3
)＜f(-1)
B、f(-1)＜f(
3
)＜f(-
2
)
C、f(
3
)＞f(-
2
)＞f(-1)
D、f(
3
)＜f(-
2
)＜f(-1)
考点：二次函数的性质
专题：函数的性质及应用
分析：关键偶函数得出；m=0，确定f（x）=-x2+3，根据单调性判断即可．
解答： 解：∵f（x）=（m-1）x2+2mx+3是偶函数，
∴m=0，
∴f（x）=-x2+3，
f（-1）=f（1），f（
2
）=f（-
2
），f（
3
）
∵f（x）在（0，+∞）单调递减，
∴f（1）＞f（
2
）＞f(
3
)，
即f（-1）＞f(-
2
)＞f(
3
)，
故选：D．
点评：本题考查了函数的奇偶性，二次函数的单调性，属于中档题．
练习册系列答案
相关题目
在平面直角坐标系xOy中，已知圆心在第二象限，半径为2
2
的圆C与直线y=x相切于坐标原点O．
（1）求圆C的方程；
（2）试探求圆C上是否存在异于原点的点Q，使Q到定点F（4，0）的距离等于线段OF的长，若存在，请求出点Q的坐标；若不存在，请说明理由．
设数列{an}满足：a1=1，a2=
5
3
，an+2=
5
3
an+1-
2
3
an（n=1，2，3，…）．
（1）令bn=an+1-an（n=1，2，3，…），求数列{bn}及{an}的通项公式；
（2）求数列{an+bn}的前n项和为Sn．
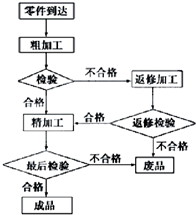某工厂加工某种零件有三道工序：粗加工，返修加工和精加工．上面是这个零件加工过程的流程图．已知这个零件最后成了废品，则最多经过了
 
道检验程序．
已知偶函数f（x），满足f（x+2）=
1
f(x)
，若f（-2）=1，则f（2014）=
 
．
已知函数f（x）=sin（ωx+φ）+b（ω＞0，-
π
2
＜φ＜
π
2
）相邻两对称轴间的距离为
π
2
，若将f（x）的图象先向左平移
π
12
个单位，再向下平移1个单位，所得的函数g（x）的为奇函数．
（1）求f（x）的解析式，并求f（x）的对称中心；
（2）若关于x的方程3[g（x）]2+m•g（x）+2=0在区间[0，
π
2
]上有两个不相等的实根，求实数m的取值范围．
已知定义在区间（-1，1）上的函数f（x）=
ax+b
1+x2
是奇函数，且f（
1
2
）=
2
5
，
（1）确定f（x）的解析式；
（2）判断f（x）的单调性并用定义证明；
（3）解不等式f（t-1）+f（t）＜0．
平面向量
a
，
b
，
e
满足：|
e
|=1，
a
•
e
=1，
.
b
•
e
=2，|
a
-
b
|=3，则
.
a
•
b
的最小值为
 
．
已知直线l过直线l1：2x-3y+2=0，l2：3x-4y-2=0的交点P，且与直线4x+y-4=0平行，
（1）求直线l的方程；
（2）求直线l与两坐标轴围成的三角形面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网