题目内容
已知函数
，正实数a、b、c满足f（c）＜0＜f（a）＜f（b），若实数d是函数f（x）的一个零点，那么下列四个判断：①d＜a；②d＞b；③d＜c；④d＞c．其中可能成立的个数为 ．
【答案】分析：根据函数零点的存在性判断方法，结合题意先求出含有零点的区间，再判断．
解答：解：由题意：正实数a、b、c满足f（c）＜0＜f（a）＜f（b），
则含有零点的区间可能为，（c，a）或（c，b），
∴函数f（x）的一个零点d，d＜a，d＜b，d＞c；则①④对
故答案为：2．
点评：本题主要考查了函数零点的存在性判断方法，结合区间判断零点的大小，是基础题．
解答：解：由题意：正实数a、b、c满足f（c）＜0＜f（a）＜f（b），
则含有零点的区间可能为，（c，a）或（c，b），
∴函数f（x）的一个零点d，d＜a，d＜b，d＞c；则①④对
故答案为：2．
点评：本题主要考查了函数零点的存在性判断方法，结合区间判断零点的大小，是基础题．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
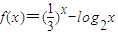，正实数a、b、c满足f（c）＜0＜f（a）＜f（b）．，若实数d是函数f（x）的一个零点，那么下列5个判断：①d＜a；②d＞b；③d＜c；④c＜a；⑤a＜b．其中可能成立的个数为（ ）
，正实数a、b、c成公差为正数的等差数列，且满足f（a）f（b）f（c）＜0，若实数d是方程f（x）=0的一个解，那么下列四个判断：①d＜a；②d＞b；③d＜c；④d＞c中，有可能成立的个数为 ．
，正实数a、b、c成公差为正数的等差数列，满足f （a） f （b） f （c）＜0，且实数d是方程f （x）=0的一个解．给出下列四个不等式：①d＜a，②d＞b，③d＜c，④d＞c，其中有可能成立的不等式的序号是 ．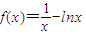
，正实数a、b、c满足f（c）＜0＜f（a）＜f（b），若实数d是函数f（x）的一个零点，那么下列四个判断：