题目内容
已知:椭圆C的中心在原点,焦点在x轴上,焦距为8,且经过点(0,3)
(1)求此椭圆的方程
(2)若已知直线l:4x-5y+40=0,问:椭圆C上是否存在一点,使它到直线l的距离最小?最小距离是多少?
解:(1)由题意知,2c=8,c=4,
∴b=3,
从而a2=b2+c2=25,
∴方程是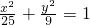 …(4分)
…(4分)
(2)由直线l的方程与椭圆的方程可以知道,直线l与椭圆不相交
设直线m平行于直线l,则直线m的方程可以写成4x-5y+k=0(1)
由方程组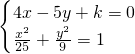
消去y,得25x2+8kx+k2-225=0(2)
令方程(2)的根的判别式△=0,得64k2-4×25(k2-225)=0(3)
解方程(3)得k1=25或k2=-25,
∴当k1=25时,直线m与椭圆交点到直线l的距离最近,此时直线m的方程为4x-5y+25=0
直线m与直线l间的距离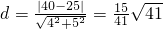
所以,最小距离是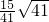 .…(8分)
.…(8分)
分析:(1)依题意可知c,根据经过点(0,3)求得b,进而根据a2=b2+c2求得a2,则椭圆方程可得;
(2)由直线l的方程与椭圆的方程可以知道,直线l与椭圆不相交,将直线l:4x-5y+40=0平移,使得其与椭圆相切,则可知切线与直线l的距离最小或最大,故设直线m平行于直线l,则直线m的方程可以写成4x-5y+k=0与椭圆方程联立,利用判别式为0可求.
点评:本题以椭圆为载体,考查椭圆的标准方程,考查点线距离,考查学生分析解决问题的能力,解题的关键是将直线l:4x-5y+40=0平移,使得其与椭圆相切,则可知切线与直线l的距离最小或最大.
∴b=3,
从而a2=b2+c2=25,
∴方程是
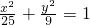 …(4分)
…(4分)(2)由直线l的方程与椭圆的方程可以知道,直线l与椭圆不相交
设直线m平行于直线l,则直线m的方程可以写成4x-5y+k=0(1)
由方程组
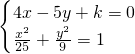
消去y,得25x2+8kx+k2-225=0(2)
令方程(2)的根的判别式△=0,得64k2-4×25(k2-225)=0(3)
解方程(3)得k1=25或k2=-25,
∴当k1=25时,直线m与椭圆交点到直线l的距离最近,此时直线m的方程为4x-5y+25=0
直线m与直线l间的距离
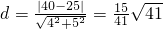
所以,最小距离是
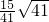 .…(8分)
.…(8分)分析:(1)依题意可知c,根据经过点(0,3)求得b,进而根据a2=b2+c2求得a2,则椭圆方程可得;
(2)由直线l的方程与椭圆的方程可以知道,直线l与椭圆不相交,将直线l:4x-5y+40=0平移,使得其与椭圆相切,则可知切线与直线l的距离最小或最大,故设直线m平行于直线l,则直线m的方程可以写成4x-5y+k=0与椭圆方程联立,利用判别式为0可求.
点评:本题以椭圆为载体,考查椭圆的标准方程,考查点线距离,考查学生分析解决问题的能力,解题的关键是将直线l:4x-5y+40=0平移,使得其与椭圆相切,则可知切线与直线l的距离最小或最大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目