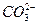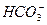题目内容
1986年,在瑞士苏黎世工作的两位科学家发现一种性能良好的金属氧化物超导体,使超导工作取得突破性进展,为此两位科学家获得1987年的诺贝尔物理学奖。这种超导材料的晶体结构如右图所示,其化学式为YBa2Cu3O7。
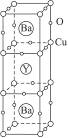
(1)已知该化合物中各元素的化合价为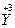 、
、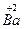 、
、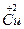 和
和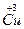 。试计算Cu在化合物中的平均化合价为______________,两种价态Cu的原子个数之比为____________。
。试计算Cu在化合物中的平均化合价为______________,两种价态Cu的原子个数之比为____________。
(2)用氧化物的形式表示该化合物的组成:____________________________________。

(1)已知该化合物中各元素的化合价为
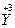 、
、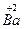 、
、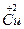 和
和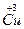 。试计算Cu在化合物中的平均化合价为______________,两种价态Cu的原子个数之比为____________。
。试计算Cu在化合物中的平均化合价为______________,两种价态Cu的原子个数之比为____________。(2)用氧化物的形式表示该化合物的组成:____________________________________。
(1)+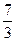
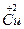 ∶
∶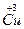 =2∶1
=2∶1
(2)Y2O3·4BaO·4CuO·Cu2O3
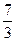
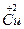 ∶
∶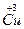 =2∶1
=2∶1(2)Y2O3·4BaO·4CuO·Cu2O3
(1)该晶体虽然是一种新型超导材料,但作为一种化合物,它同样满足化学式中“正负化合价代数和为零”的原则,据此计算出Cu的平均化合价为+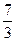 ;因为
;因为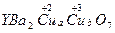 ,则有:a+b=3,2a+3b=7。联立方程解得a=2,b=1。即
,则有:a+b=3,2a+3b=7。联立方程解得a=2,b=1。即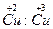 =2∶1。(2)根据Y、Ba、Cu的化合价,其氧化物的化学式为Y2O3、BaO、CuO、Cu2O3,因Cu的+2、+3两种价态的原子个数之比为2∶1,所以推得n(CuO)∶n(Cu2O3)= 4∶1。即该化合物的组成可表示为Y2O3·4BaO·4CuO·Cu2O3。
=2∶1。(2)根据Y、Ba、Cu的化合价,其氧化物的化学式为Y2O3、BaO、CuO、Cu2O3,因Cu的+2、+3两种价态的原子个数之比为2∶1,所以推得n(CuO)∶n(Cu2O3)= 4∶1。即该化合物的组成可表示为Y2O3·4BaO·4CuO·Cu2O3。
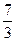 ;因为
;因为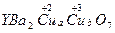 ,则有:a+b=3,2a+3b=7。联立方程解得a=2,b=1。即
,则有:a+b=3,2a+3b=7。联立方程解得a=2,b=1。即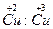 =2∶1。(2)根据Y、Ba、Cu的化合价,其氧化物的化学式为Y2O3、BaO、CuO、Cu2O3,因Cu的+2、+3两种价态的原子个数之比为2∶1,所以推得n(CuO)∶n(Cu2O3)= 4∶1。即该化合物的组成可表示为Y2O3·4BaO·4CuO·Cu2O3。
=2∶1。(2)根据Y、Ba、Cu的化合价,其氧化物的化学式为Y2O3、BaO、CuO、Cu2O3,因Cu的+2、+3两种价态的原子个数之比为2∶1,所以推得n(CuO)∶n(Cu2O3)= 4∶1。即该化合物的组成可表示为Y2O3·4BaO·4CuO·Cu2O3。
练习册系列答案
相关题目
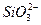 +CO2+H2O====H2SiO3↓+
+CO2+H2O====H2SiO3↓+