Question

15．

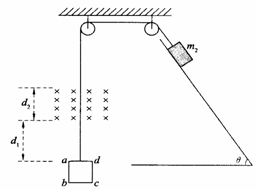
(扬州期末15分)如图所示，一边长L = 0.2m，质量m₁ = 0.5kg，电阻R = 0.1Ω的正方形导体线框abcd，与一质量为m₂ = 2kg的物块通过轻质细线跨过两定滑轮相连。起初ad边距磁场下边界为d₁ = 0.8m，磁感应强度B=2.5T，磁场宽度d₂ =0.3m，物块放在倾角θ=53°的斜面上，物块与斜面间的动摩擦因数μ=0.5。现将物块由静止释放，经一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动。（g取10m/s²，sin53°=0.8，cos53°= 0.6）求：

   （1）线框ad边从磁场上边缘穿出时绳中拉力的功率；

   （2）线框刚刚全部进入磁场时速度的大小；

   （3）整个运动过程中线框产生的焦耳热。

Answer 1

1,3,5

解：

1,3,5

（1）由于线框匀速出磁场，则

对m₂有：

得T=10N   ……2分

对m₁有：

又因为

联立可得：……2分

所以绳中拉力的功率P=Tv=20W   ……2分

 （2）从线框刚刚全部进入磁场到线框ad边刚要离开磁场，由动能定理得

 ……3分

且

解得v₀==1.9m/s……2分

   （3）从初状态到线框刚刚完全出磁场，由能的转化与守恒定律可得

将数值代入，整理可得线框在整个运动过程中产生的焦耳热为：

Q = 1.5 J  ……1分

感悟与反思：

第一问学生往往错误地应用整体法而得出错误答案；第二问有两种解法，一是利用能量转化与守恒，二是纯粹用运动学方法解，但必须正确隔离两个物体；第三问似与第二问考点重复，删去也可。