题目内容
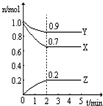
 某温度时,在一个2L的密闭容器中,X、Y、Z三种气体物质的物质的量随时间的变化曲线如图所示.根据图中数据,试填写下列空白:
某温度时,在一个2L的密闭容器中,X、Y、Z三种气体物质的物质的量随时间的变化曲线如图所示.根据图中数据,试填写下列空白:(1)该反应第
2
2
分钟到达平衡状态,X所占的体积分数为38.9%
38.9%
.(2)该反应的化学方程式为
3X+Y 2Z
2Z
 2Z
2Z3X+Y 2Z
2Z
. 2Z
2Z(3)反应开始至2min,气体X的平均反应速率为
0.075mol/(L?min)
0.075mol/(L?min)
.分析:(1)根据曲线的变化特点判断达到平衡的时间,根据平衡时各种物质的物质的量计算物质的量分数,即体积分数;
(2)根据曲线的变化趋势判断反应物和生成物,根据物质的量变化之比等于化学计量数之比书写方程式;
(3)根据v=
计算反应速率.
(2)根据曲线的变化趋势判断反应物和生成物,根据物质的量变化之比等于化学计量数之比书写方程式;
(3)根据v=
| △c |
| △t |
解答:解析:(1)从图象来看,第2分钟各物质的物质的量不再发生变化,因此第2分钟到达平衡状态,X所占体积分数为
×100%=38.9%,
故答案为:2;38.9%;
(2)从曲线的变化趋势可以看出,从反应开始到达到平衡,X、Y的物质的量减少,应为反应物,Z的物质的量增加,应为生成物,从反应开始到第2分钟反应到达平衡状态,X、Y消耗的物质的量分别为0.3 mol、0.1 mol,Z的生成的物质的量为0.2 mol,因此三者比例为3:1:2,
物质的量变化之比等于化学计量数之比,则化学方程式为3X+Y 2Z,
2Z,
故答案为:3X+Y 2Z;
2Z;
(3)v=
=
=0.075mol/(L?min),
故答案为:0.075mol/(L?min).
| 0.7mol |
| (0.7+0.9+0.2)mol |
故答案为:2;38.9%;
(2)从曲线的变化趋势可以看出,从反应开始到达到平衡,X、Y的物质的量减少,应为反应物,Z的物质的量增加,应为生成物,从反应开始到第2分钟反应到达平衡状态,X、Y消耗的物质的量分别为0.3 mol、0.1 mol,Z的生成的物质的量为0.2 mol,因此三者比例为3:1:2,
物质的量变化之比等于化学计量数之比,则化学方程式为3X+Y
 2Z,
2Z,故答案为:3X+Y
 2Z;
2Z;(3)v=
| △c |
| △t |
| ||
| 2min |
故答案为:0.075mol/(L?min).
点评:本题考查物质的量随时间的变化曲线,题目难度不大,本题注意化学方程式的判断方法.

练习册系列答案
相关题目
 某温度时,在一个2L的密闭容器中,X、Y、Z三种物质的物质的量随时间的变化曲线如图所示.根据图中数据,试填写下列空白:
某温度时,在一个2L的密闭容器中,X、Y、Z三种物质的物质的量随时间的变化曲线如图所示.根据图中数据,试填写下列空白: 2 Z
2 Z
 2Z
2Z 某温度时,在一个2L的密闭容器中,X、Y、Z三种物质的物质的量随时间的变化曲线如图所示.根据图中数据填空:
某温度时,在一个2L的密闭容器中,X、Y、Z三种物质的物质的量随时间的变化曲线如图所示.根据图中数据填空: 2Z
2Z 某温度时,在一个2L的密闭容器中,X、Y、Z三种气态物质的物质的量随时间的变化曲线如图所示.下列说法在不正确的是( )
某温度时,在一个2L的密闭容器中,X、Y、Z三种气态物质的物质的量随时间的变化曲线如图所示.下列说法在不正确的是( )