题目内容
1996年诺贝尔化学奖授予对发现C60有重大贡献的三位科学家。C60分子是形如球状的多面体，如右图，该结构的建立基于以下考虑：C60分子中每个碳原子只跟相邻的3个碳原子形成化学键；C60分子只含有五边形和六边形；碳与碳之间既有单键又有双键，每个碳原子仍然满足四个价键饱和；多面体的顶点数、面数和棱边数的关系，遵循欧拉定理：顶点数+面数-棱边数=2。
请完成下列问题：
(1)一个C60分子中有多少个五边形和多少个六边形？
(2)一个C60分子中有多少个C=C？
(3)已知C70分子的结构模型也遵循C60的那些规律，请确定C70分子结构中上述几项参数。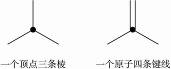
请完成下列问题：
(1)一个C60分子中有多少个五边形和多少个六边形？
(2)一个C60分子中有多少个C=C？
(3)已知C70分子的结构模型也遵循C60的那些规律，请确定C70分子结构中上述几项参数。
(1)一个C60分子中有12个五边形和20个六边形。
(2)一个C60分子中有30个C=C。
(3)C70分子结构中的五边形和六边形的个数分别为12、25，C—C单键数和C=C双键数分别为70、35。
(2)一个C60分子中有30个C=C。
(3)C70分子结构中的五边形和六边形的个数分别为12、25，C—C单键数和C=C双键数分别为70、35。
(1)设C60分子中含有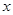
个五边形和
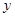个六边形。?
先求欧拉定理中棱边数：每个顶点伸出三条棱，而每条棱又总是由两个顶点共有，所以，每个顶点单独伸出的棱有3×1/2=1.5条，60个顶点共伸出的棱为60×1.5=90条。至此，依据欧拉定理可写出：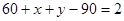
①
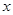为了求出和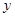，还要建立一个方程式。因为五边形和六边形构成多面体时是共用棱边和顶点的，所以，还可以根据棱边数守恒和顶点数守恒写出两个方程式。
棱边数守恒：每条棱是由两个多面体共用的，所以，一个五边形单独占有的棱边数为5/2=2.5条，一个六边形单独占有的棱边数为6/2=3条，所以，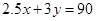
②
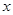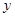至此联立①②可以解得：=12，=20。
(2)首先要明确一个概念：在图中顶点间形成的棱都以单线标出，但有的是表示单键，有的是表示双键。从空间结构来说，每个碳原子连接三条棱，而从化学价键来说，每个碳原子连接四条键线。(一个双键也只是一个键，可以说有两条键线但不能说是两个键)。设一个C60分子中含的C—C单键数和C=C双键数分别为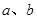
，则根据棱边守恒有：
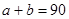④
再利用键线守恒列一个方程式。每个原子连接四条键线而每条键线被两个原子所共有，所以，每个原子单独占有的键线数为4/2=2，所以，60个碳原子共有键线120条：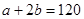
⑤
联立④⑤解得：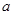
=60，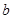
=30。即C60中含的双键数为30。
(3)设C70分子结构中的五边形和六边形的个数分别为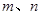
，设C—C单键数和C=C双键数分别为
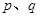，则一个C70分子中的棱边总数为70×1.5=105；依据欧拉定理有：
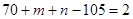⑥；依据顶点数守恒有：
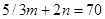⑦；联立⑥⑦得：
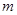=12,
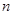=25。?
根据棱边守恒又写出：
=105 ⑧；根据键线守恒有：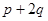
=70×2=140 ⑨；联立⑧⑨得：
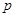=70，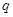
=35。即C70中含的双键数为35。
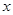个五边形和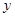个六边形。?先求欧拉定理中棱边数：每个顶点伸出三条棱，而每条棱又总是由两个顶点共有，所以，每个顶点单独伸出的棱有3×1/2=1.5条，60个顶点共伸出的棱为60×1.5=90条。至此，依据欧拉定理可写出：
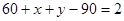①为了求出
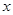和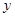，还要建立一个方程式。因为五边形和六边形构成多面体时是共用棱边和顶点的，所以，还可以根据棱边数守恒和顶点数守恒写出两个方程式。棱边数守恒：每条棱是由两个多面体共用的，所以，一个五边形单独占有的棱边数为5/2=2.5条，一个六边形单独占有的棱边数为6/2=3条，所以，
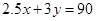②至此联立①②可以解得：
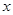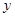=12，=20。(2)首先要明确一个概念：在图中顶点间形成的棱都以单线标出，但有的是表示单键，有的是表示双键。从空间结构来说，每个碳原子连接三条棱，而从化学价键来说，每个碳原子连接四条键线。(一个双键也只是一个键，可以说有两条键线但不能说是两个键)。设一个C60分子中含的C—C单键数和C=C双键数分别为
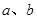，则根据棱边守恒有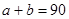： ④再利用键线守恒列一个方程式。每个原子连接四条键线而每条键线被两个原子所共有，所以，每个原子单独占有的键线数为4/2=2，所以，60个碳原子共有键线120条：
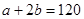⑤联立④⑤解得：
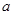=60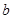， =30。即C60中含的双键数为30。(3)设C70分子结构中的五边形和六边形的个数分别为
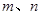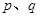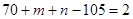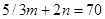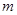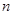，设C—C单键数和C=C双键数分别为，则一个C70分子中的棱边总数为70×1.5=105；依据欧拉定理有： ⑥；依据顶点数守恒有： ⑦；联立⑥⑦得：=12,=25。?根据棱边守恒又写出：
=105 ⑧；根据键线守恒有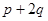：=70×2=140 ⑨；联立⑧⑨得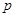：=70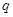，=35。即C70中含的双键数为35。
练习册系列答案
相关题目
