题目内容
17.某温度下,容积同为2L的3个密闭容器中,按不同方式投入反应物,保持恒温、恒容,测得反应达到平衡时的有关数据如下(已知某温度下2HI(g)?H2(g)+I2(g)△H=+AkJ•mol-1 K=4.0)
| 容器 | 甲 | 乙 | 丙 |
| 反应物投入量 | 2 mol HI | 1mol H2+1mol I2 | 2mol HI+1mol H2+1mol I2 |
| HI的浓度 | c1 | c2 | c3 |
| 反应的能量变化 | 吸收akJ | 放出bkJ | 吸收ckJ |
| 体系压强(Pa) | p1 | p2 | p3 |
| 反应物转化率 | a1 | a2 | a3 |
①c1、c3的关系式为2c1=c3
②a、b的关系式为a+b=A
③p2、p3的关系式为2p2=p3
④a1与a2的关系式为α1+α2=1
(2)甲容器中:该反应的平衡常数表达式为K=$\frac{c({H}_{2})•c({I}_{2})}{{c}^{2}(HI)}$.
(3)乙容器中:反应在开始2分钟后达平衡状态,则该反应在这2分钟内用HI表示的平均反应速率为0.1mol•L-1•min-1
(4)丙容器中:反应开始时V正大于V逆(填“小于”、“等于”或“大于”)
分析 1)2HI(g)?H2(g)+I2(g)该反应中反应前后气体体积不变,则压强不影响平衡,甲、乙、丙都互为等效平衡,达到平衡时各组分的含量、反应物转化率一定相等,其中甲与乙为完全等效平衡,各组分的浓度、百分含量完全相同,而丙中达到平衡时各组分的浓度为甲和乙的2倍,据此判断c1与c3、p2与p3、α1与α2、a与b关系;
(2)根据平衡常数的概念并结合该反应方程式写出该反应的平衡常数表达式;
(3)设出得到平衡时HI的浓度变化,然后利用三段式及该反应的化学平衡常数k=4列式计算出HI的浓度变化,然后根据反应速率的表达式v=$\frac{△c}{△t}$表示出用HJI表示的反应速率;
(4)根据该反应为吸热反应,而丙中达到平衡时吸收热量进行判断移动方向,再判断正、逆反应速率大小.
解答 解:(1)2HI(g)?H2(g)+I2(g)该反应中反应前后气体体积不变,则压强不影响平衡,甲、乙、丙都互为等效平衡,达到平衡时各组分的含量、反应物转化率一定相等,其中甲与乙为完全等效平衡,各组分的浓度、百分含量完全相同,而丙中达到平衡时各组分的浓度为甲和乙的2倍,
①甲和丙互为等效平衡,由于丙中相当于加入了4mol碘化氢,则达到平衡时c1、c3的关系式为:2c1=c3,
故答案为:2c1=c3;
②甲和乙为从两个方向进行的完全等效平衡,则达到平衡时a、b的关系式为:a+b=A,
故答案为:a+b=A;
③甲和乙为完全等效平衡,则丙的初始反应物的物质的量相当于乙的2倍,则达到平衡时p2、p3的关系式为:2p2=p3,
故答案为:2p2=p3;
④甲和乙为从两个方向进行的完全等效平衡,则甲中转化率与乙中转化率之和一定为1,即α1与α2的关系式为:α1+α2=1,
故答案为:α1+α2=1;
(2)反应2HI(g)?H2(g)+I2(g)的平衡常数表达式为:K=$\frac{c({H}_{2})•c({I}_{2})}{{c}^{2}(HI)}$,
故答案为:K=$\frac{c({H}_{2})•c({I}_{2})}{{c}^{2}(HI)}$;
(3)设得到平衡状态时HI的浓度变化为x,
2HI(g)?H2(g)+I2(g)
开始 0 0.5 0.5
变化 x 0.5x 0.5x
平衡 x 0.5-0.5x 0.5-0.5x
根据该温度下化学平衡常数K=4可得:K=$\frac{(0.5-0.5x)×(0.5-0.5x)}{{x}^{2}}$=4,解得:x=0.2mo/L,
则该反应在这2分钟内用HI表示的平均反应速率为:v(HI)=$\frac{0.2mol/L}{2min}$=0.1mol•L-1•min-1,
故答案为:0.1mol•L-1•min-1;
(4)丙中达到平衡时吸收ckJ,反应2HI(g)?H2(g)+I2(g)△H=+A kJ•mol-1为吸热反应,所以开始时丙向右移动,则正反应速率大于逆反应速率,
故答案为:大于.
点评 本题考查了化学平衡常数的计算,题目难度中等,明确化学平衡及其影响因素为解答关键,注意掌握三段式在化学平衡计算中的应用方法,试题培养了学生的分析能力及化学计算能力.

| A. | X均能形成化学式为HXO3的酸 | |
| B. | X均能与某些金属元素形成化合物 | |
| C. | X原子的最外层电子数和核电荷数肯定为奇数 | |
| D. | X不可能形成化学式为KXO4的盐 |
| A. | 太阳能、氢能、风能、生物质能都属于新能源 | |
| B. | 常温下,反应C(s)+CO2(g)=2CO(g)不能自发进行,则该反应的△H<0 | |
| C. | 人们通常用标准燃烧热或热值来衡量燃料燃烧放出热量的大小,某物质的热值越高则其标准燃烧热越大 | |
| D. | 镀层破损后,马口铁比白铁更耐腐蚀 |
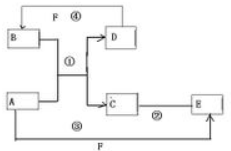 A、B、C、D、E、F六种物质的相互转化关系如图所示(反应条件均未列出).
A、B、C、D、E、F六种物质的相互转化关系如图所示(反应条件均未列出).
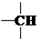 和一个-Cl,它的可能结构分别是(填写结构简式):CH3CH2CH2CHClCH3、CH3CH2CHClCH2CH3、CH3CH(CH3)CH2CH2Cl、CH2ClCH(CH3)CH2CH3.
和一个-Cl,它的可能结构分别是(填写结构简式):CH3CH2CH2CHClCH3、CH3CH2CHClCH2CH3、CH3CH(CH3)CH2CH2Cl、CH2ClCH(CH3)CH2CH3.