题目内容
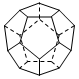
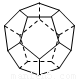
 德国和美国科学家首先制出由20个碳原子组成的空心笼状分子C20,该笼状结构是由许多正五边形构成(如图).请回答:C20分子共有
德国和美国科学家首先制出由20个碳原子组成的空心笼状分子C20,该笼状结构是由许多正五边形构成(如图).请回答:C20分子共有12
12
个正五边形,共有30
30
条棱边,C20晶体属于分子晶体
分子晶体
(填晶体类型).分析:利用均摊法分析晶体结构,每个碳原子被3个正五边形共用,所以每个正五边形中含有5×
个,根据原子守恒计算五边形个数.
| 1 |
| 3 |
解答:解:从分子结构示意图可以看出,在C20分子内每个碳原子与另外3个碳原子成键,因此,C20分子键总数=20×3×
(因为2个原子形成一个键),也即C20分子中共有30条棱边(因为化学键总数=多面体棱边总数).从数学角度,多面体棱边数=多面体面数×每个面的棱边数×
(因为2个面共用一条棱边),设正五边形的个数为x,则有30=x×5×
,所以,正五边形的个数为12,实际上C20与C60都属于碳的同素异形体,应属于分子晶体;
解法二:设C20分子中含x个正五边形,通过观察图形可知,每一个顶点为三个正五边形共用,则每个正五边形占有该顶点的
,因此,每个正五边形占有碳原子数为5×
个,这个基本结构单元的碳原子数为x×5×
=20,因此,C20分子中含有正五边形个数x=12;每一条边为两个正五边形共用,每个正五边形只占有这条边的,故C-C键的数目为12×5×
=30个,即C20分子中共有30条棱边,
故答案为:12;30;分子晶体.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解法二:设C20分子中含x个正五边形,通过观察图形可知,每一个顶点为三个正五边形共用,则每个正五边形占有该顶点的
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
故答案为:12;30;分子晶体.
点评:本题考查了晶胞的计算,解答时注意利用均摊法结合数学知识分析晶体的结构,难度较大.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目