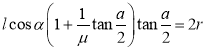题目内容
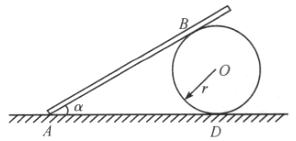
【题目】如图所示,均质杆![]() 长为
长为![]() ,
,![]() 端用球形铰固定,
端用球形铰固定,![]() 端置于半径为
端置于半径为![]() 的球面上(图为
的球面上(图为![]() 球面),杆与球面间的摩擦因数为
球面),杆与球面间的摩擦因数为![]() ,球心至
,球心至![]() 端距离
端距离![]() ,试求
,试求![]() 平衡时,
平衡时,![]() 连线与
连线与![]() 轴所成的最大夹角.
轴所成的最大夹角.

【答案】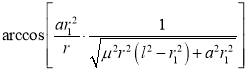 ,
,
式中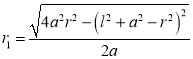
【解析】
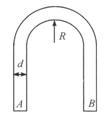
因杆的![]() 端置于球面上,则
端置于球面上,则![]() 任何时候都满足图乙所示的位置关系,其中
任何时候都满足图乙所示的位置关系,其中
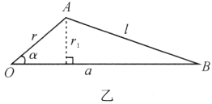
![]() ,
,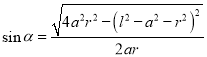 .
.
设![]() 连线与
连线与![]() 轴所成的夹角最大时,
轴所成的夹角最大时,![]() 在
在![]() 坐标中的方向角为
坐标中的方向角为![]() ,则
,则![]() 点坐标为
点坐标为![]() .
.
当![]() 点在球面上移动时,其轨迹的圆心
点在球面上移动时,其轨迹的圆心![]() 在
在![]() 轴上,设
轴上,设![]() 与
与![]() 轴方向的夹角为
轴方向的夹角为![]() ,
,![]() ,则
,则![]() ,
,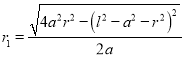 .
.
取过![]() 且平行于
且平行于![]() 轴的直线为转轴,则由力矩平衡得
轴的直线为转轴,则由力矩平衡得![]() .
.
又在临界状态有![]() ,所以,
,所以,![]() .
.
因为![]() ,所以,
,所以,![]() .
.
代入相关的值有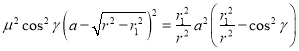 ,
,
整理得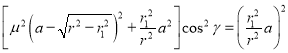 ,
,
所以,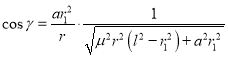 ,
,
所以,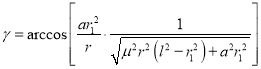 ,式中
,式中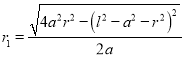 .
.
俗话说:方向不对,功夫白费. 经验表明,此话是可以用于本题的.
物理试题中,有很大一部分试题的题干是图,文配合的,很多人在审题时,或望图生义,或望文生义,忽略了图、文之间的相互补充与相互制约,在不知不觉中对题干条件作了修改,可想而知,继续下去的结果会是什么?
在解答本题时,很多同学在看到示意图后,不假思索地认为,杆子是搭放在球面上的,即杆与球面相切,因为这种模型太常见了. 有了这种先入为主的惯性思维后,不再认真思考题文中关于杆的![]() 端置于球面上的约束,据此思路做下去,也许一路顺畅,但却是“功夫白费”.
端置于球面上的约束,据此思路做下去,也许一路顺畅,但却是“功夫白费”.
本题的解答过程中,用到空间解析几何的有关知识点,对于这种高中常规数学中没有涉及的知识点,作为物理竞赛的学习者,是必须通过自我的学习进行补充的.

练习册系列答案
相关题目