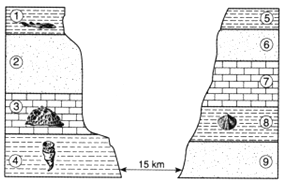
题目内容
【题目】如图所示,半径R的均匀圆木在水平地面上以平动速度![]() 做匀速滚动时,与高h的台阶相遇,接触处发生完全非弹性碰撞,即在碰撞后图中圆木与台阶侧棱接触部位A的速度降为零。再设两者间的摩擦因数足够大,使得部位A不会与台阶侧棱在而后的接触过程中发生相对滑动。
做匀速滚动时,与高h的台阶相遇,接触处发生完全非弹性碰撞,即在碰撞后图中圆木与台阶侧棱接触部位A的速度降为零。再设两者间的摩擦因数足够大,使得部位A不会与台阶侧棱在而后的接触过程中发生相对滑动。
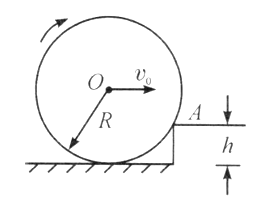
(1) ![]() 和h取何值时,圆木能绕侧棱滚上台阶?
和h取何值时,圆木能绕侧棱滚上台阶?
(2)在(1)问基础上,确定部位A与侧棱间摩擦因数![]() 的取值范围。
的取值范围。
【答案】(1)![]() (2)
(2)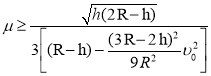
【解析】
(1)碰撞前圆木的转动角速度为
![]() .
.
碰后瞬间圆木转动角速度记为![]() ,因碰撞前后相对侧棱角动量守恒,故有
,因碰撞前后相对侧棱角动量守恒,故有
![]() ,
,
![]() ,
,
其中m为圆木质量。
可解得![]() 。
。
而后的定轴转动过程中机械能守恒,为能滚上台阶,首先要求
![]() .
.
即得![]() 。
。
过程中除了摩擦因数足够大,确保A与侧棱间无相对滑动,还要求侧棱指向圆木中心的法向支持力N始终大于零。如图乙所示,将转动过程中角速度记为![]() ,则有
,则有

![]() .
.
上滚时,![]() 增大,
增大,![]() 增大,
增大,![]() 减小(因势能增大,动能减小),故N增大。可见,N在转动的最初时刻最小。于是,要求
减小(因势能增大,动能减小),故N增大。可见,N在转动的最初时刻最小。于是,要求
![]() ,
,
即要求![]() 。
。
综上所述,![]() 可取范围为
可取范围为
![]() .
.
为使上式能满足,还要求
![]() ,
,
即得h可取范围为![]() 。
。
(2)相对台阶侧棱的转动定理公式为
![]() .
.
角加速度沿逆时针方向,已在图中示出.若取质心系中质心为参考点,转动定理公式又为
![]() ,
,
其中,f是侧棱提供的摩擦力,方向也已在图中示出,于是可得
![]() .
.
圆木上滚时,![]() 增大,N增大,f减小,故
增大,N增大,f减小,故![]() 减小.可见,
减小.可见,![]() 在转动的最初时刻最大,因此
在转动的最初时刻最大,因此
![]() ,
,
式中![]()
![]() ,
,
![]()
![]() .
.
![]() 的可取范围为
的可取范围为
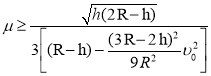 .
.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目