Question

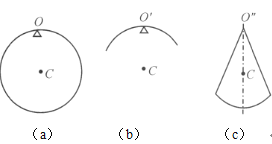
【题目】如图所示三个摆，其中图（a）是半径为的匀质细圆环，悬挂在点并可绕此点且垂直于纸面的轴线摆动，图（b）、图（c）是同样圆环中对轴对称截取的一部分，分别悬挂在点和点，可各绕过点和点且垂直于纸面的轴线摆动，如悬线的质量不计，摆角都不大，比较它们的摆动周期.

Answer 1

【答案】三种情况的摆动周期相等.

【解析】

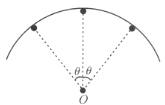
以图（b）的情况为例进行讨论.

如图所示，设环的质量为，在圆弧左右对称处角处取两质元，则这一部分绕转轴的转动惯量为

，

.

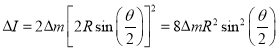则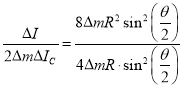，与无关.

说明对于整段圆弧，仍有.

则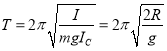，与无关.

对（a）取即可，而（c）对应于的情形，所以，三种情况的摆动周期相等.

看上去，三个复摆的差异是很明显的，如无分析它们共性特征的能力，必然会一个一个地求解，耗时费力不说，出错的概率也会随之增加.本题的解答让我们见识了透过现象看本质的能力对解题带来的积极效果.当然，本题的结果也让我们积累了认识此类问题本质的能力.

一道习题同时列出几个类似的模型，实际上也是在暗示我们，它们之间有相通之处，寻找它们的共同点会为我们的解答带来便利，提升我们透过现象看本质的能力.