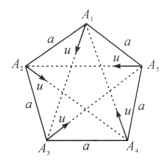
题目内容
【题目】各边长为a的正五边形的五个顶点各有一个质点，分别为
、
、
、
和
，如图所示。今使质点始终对准质点运动，始终对准运动，始终对准运动，始终对准运动，始终对准运动，运动速率均为相同的u。试问：经多长时间t，五个质点相聚？
【答案】
【解析】
方法1：各边长为a的正五边形的五个顶点处各有一个质点,分别为
、
、
、
和
,如图所示。今使质点始终对准质点运动,始终对准运动,始终对准运动,始终对准运动,始终对准运动,运动速率均为相同的u.试问:经多长时间t，五个质点相聚？
方法2：本题的解法有很多,此处仅提供下面的解答。
由对称性知,质点的最终相遇点必在正五边形的中心点O,如图所示。
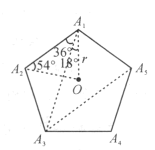
开始时质点到O点的距离为
。
由质点的运动特征易知,任何时候,质点指向O点的运动速度为
。
所以,质点相遇的总时间为
。
与本题类似的追逐问题在各类竞赛资料中有很多,基本都是三体相互追逐的翻版,其处理方法也有很多种,核心是相对运动的速度与对应的路程的求解.如通过速度的分解求出两相邻的质点间的接近速度,亦易得到相遇的时间;抑或通过微元过程来分析相互接近的速度等。
本题还有一个非常有意思的延伸问题:任一质点在到达O点之前,绕O点转过的圈数是多少?有兴趣的同学不妨试着解答一下。
练习册系列答案
阅读快车系列答案
相关题目
