题目内容
【题目】4只蜗牛在一个非常大的平台上各自做匀速直线运动，其运动路径的方向是随机的（但是没有平行的，也就是说任何两只蜗牛都有可能相遇），但是没有任何两只以上的蜗牛的路径会相交于一点。如果4只蜗牛可能相遇的
次中的5次已经发生，我们是否可以预言第六次相遇能否发生？
【答案】不能
【解析】
方法1我们首先来考虑三只蜗牛彼此相遇的情况。
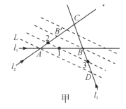
将蜗牛编号为1、2、3,它们在平面上的轨迹分别为
、
、
，其运动方向如图甲中箭头所示。
若三只蜗牛能相遇,则它们只能相遇于A、B、C三点，设1号与2号相遇于A点时,3号此时还在D点,设A、D的连线为L,3号与1号和2号分别相遇于B点与C点,由于三只蜗牛都是做匀速运动的,那么2号运动AC这段距离的时间与3号运动DC这段距离的时间相等,由此可以作如下推断,当1号与3号相遇于B点时,2号在
点,由时间关系
及匀速运动的规律易推得：
，可得；
；同样可推得：2号与3号相遇于C点时,1号的位置与C点的连线应与直线AD平行.依此类推可得出:
三只蜗牛在运动过程中,它们任意时刻所在位置的连线都是与图甲中的直线L平行的,如图中的虚线与、、的交点位置就是它们各个时刻的位置也就是说,如果三只蜗牛能彼此相遇,它们任意时刻必定在同一直线上,如图中的1、2、3点。
下面我们再回到4只蜗牛相遇的问题上。
将四只蜗牛编号为1、2、3、4,若它们的6次可能相遇中,只剩下3号与4号还没有相遇,那么,由于1、2、3这三只蜗牛彼此相遇过,由前面的论述可知,这三只蜗牛必定在同一直线上;同理,由于2、3、4这三只蜗牛彼此相遇过,它们也必然在同一条直线上,由此可以确定,这四只蜗牛也必定在同一直线上,并且,这条直线在垂直于该直线方向上是匀速平移的。
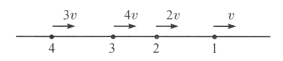
如果我们以这四只蜗牛所在的直线做参照,那么,这四只蜗牛只能是在这条直线上运动,这样,我们就很容易确定,当它们6次可能相遇中的5次已经发生后,剩下的一次能否相遇则取决于我们开始记录蜗牛相遇时,蜗牛最初的位置,即问题的初态.我们不妨设置图乙所示的情况,1、23、4四只蜗牛在同一直线上向同一方向运动,其速度大小分别为
、
、
、
，如果我们研究的最初位置如图乙所示,或者说蜗牛从图乙所示的位置开始运动,我们不难发现最初的5次相遇是能够发生的,但3号与4号蜗牛则没有相遇的机会;但如果在初态时将3号与4号的位置交换(这是可能的),那么,它们必定会相遇6次,也就是说,第6次相遇是可能发生的。
方法2：设四只蜗牛运动的平面为平面
，在此基础上引入时间轴t,建立三维坐标
，则蜗牛在任一时刻t在平面上的位置可以通过三维坐标(时空坐标)进行描述.如三维坐标中的点
所描述的就是在时刻t蜗牛在
平面内的位置
，如图所示。
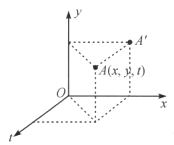
由于每只蜗牛的运动均为匀速直线运动,则蜗牛的位移与时间的关系是线性的,所以,每只蜗牛的运动轨迹在坐标内为一空间直线。
设四只蜗牛的轨迹分别为直线、、、
，两条直线的交点说明两只蜗牛在同一时刻到达同一位置,即两只蜗牛相遇.我们不妨设最后一次待证的相遇为、的交点,则由、、两两相交可知，、、一定在同一平面内(这一平面为一空间平面)，同理，由、、的两两相遇,也可确定、、也一定在同一平面内,因蜗牛的运动轨迹不能平行,即、不平行,即可确定、、、必定共面,加之、也不能平行,则、必定存在着一个交点,即这两只蜗牛在同一时刻到达平面上的同一点,它们应该“相遇”。
问题是我们应该考虑实际情况,蜗牛的运动不可能是无边界的,作为研究的起点,其相遇点的时间坐标应该满足
。所以,若、交点的时间坐标，则说明第6次相遇能够发生;若、交点的时间坐标
，则说明在实际中,这两只蜗牛是不能再相遇的,亦即第6次相遇不能发生。
本题看似条件不是十分充分,但只要能将相遇的条件理解透彻,其相对运动模型还是十分清晰的.但第6次相遇能否发生取决于初始条件,这需要讨论,而这一点往往会令答题者举棋不定。
对于方法2用一个空间直线模型来处理相遇问题,思维独到,也更能清晰地说明问题,其能力要求自然更高。
