题目内容
【题目】设有频率相同，振动方向相同的两简谐振动，位移分别为
，
．试求它们的合振动．
【答案】
．根据矢量合成法则，容易求得
，
．
【解析】
合振动为
接下去可用三角函数变换的方法求得结果，但比较烦琐。这里我们应用振动矢量图来求解，简单明了，且物理意义清晰。
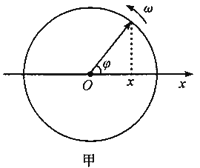
首先介绍一下表示简谐振动的矢量图（图甲）．设有简谐振动．
我们作一旋转振动矢量，其始点位于x轴坐标原点，模为A，绕原点以角速度
转动。设初始时刻
．矢量与x轴夹角为
，则任一时刻t，失量在x轴上投影为．
可见，这一旋转矢量正是简谐振动的一种合理表示．此图像通常称为简谐振动矢量图，如图乙所示。以下我们借助于矢量图来进行矢量振动合成．
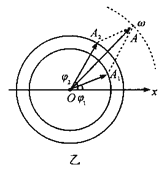
既然简谐振动可用矢量表示，则简谐振动的合成，亦即矢量的合成．作原点重合的两旋转失量
、
，分别表示两简谐振动，得
，
则合矢量
，便可表示合运动
．由于、以相同的角频率绕共同原点旋转，相对位置不变，故合矢量A也以同样的角频率旋转，且模不变，故合运动必定也是同方向同频率的简谐振动，如图丙所示。
．
根据矢量合成法则，容易求得（如图丙所示）
，．
练习册系列答案
相关题目
