[题目](1)将一个三棱柱的各面延展成平面后,这些平面可将空间分成几部分?(2)将一个三棱锥的各面延展成平面后,这些平面可将空间分成几部分? 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】（1）将一个三棱柱的各面延展成平面后,这些平面可将空间分成几部分?

（2）将一个三棱锥的各面延展成平面后,这些平面可将空间分成几部分?

【答案】见解析

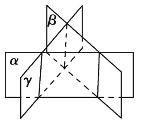
【解析】（1）如图,将三棱柱的三个侧面延展成平面后,可将空间分成7部分,然后将三棱柱的两底面延展成平面,那么每一个平面将这7部分一分为二,故共分成3×7=21部分.

（2）如图,将三棱锥的各面延展成平面后,三棱锥的内部是一个空间；将平面ABD，平面ABC，平面ACD延展后，在平面BCD的下方会分割出一个空间,也说是平面BCD对应一个空间，同理，平面ABD，平面ABC，平面ACD也各对应一个空间，这样的空间共有4个；

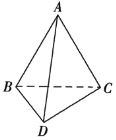
同样,将上述三个平面延展后,在顶点A的上方,也分割出一个空间,也就是顶点A对应一个空间,同理,顶点B,C,D也各对应一个空间,这样的空间共有4个;

将三棱锥的各面延展后,棱AB将对应几何体外部的一个空间,同理,其余的5条棱也各对应类似的一个空间,这样的空间共有6个.

因此三棱锥的各面延展成平面后,可将空间分成1+4+4+6=15部分.

练习册系列答案

据此完成下面小题。

【1】导致珠三角和长三角部分城市发生收缩的原因最可能是

A.地理位置偏远B.自然资源短缺

C.产业升级D.城市规模过大

【2】收缩型城市未来的发展方向有

①调整产业结构

②重视城镇老旧小区改造工作

③与周边大小城市共同建设成长

④扩大城市面积

A.①②③B.②③④

C.①③④D.①②④

【题目】湘潭高新区成立于1992年，2014年获批长株潭国家自主创新示范区。这里入驻近千家企业，重点围绕智能技术研发、能源装备、新材料、现代服务业、3D 打印与大数据等产业着力打造。2015年湘潭高新区启动湖南省首家院士创新产业园建设工作，目前该高新区已经研发了消防机器人、安保机器人、智能型服务机器人等11种适用于不同行业的特种机器人。据此完成下面小题。

【1】湘潭高新区吸引众多企业入驻的主要原因是（）

A.利用当地丰富的能源B.共用当地的基础设施

C.促进当地的经济发展D.解决当地的就业问题

【2】湘潭高新区特种机器人产业发展迅速的有利区位条件主要是（）

A.地价便宜B.原材料供应充足C.市场竞争力小D.研发投入大

【题目】判定下列函数的奇偶性．

（1）f（x）＝；

（2）f（x）＝；

（3）f（x）＝；

（4）f（x）＝|x＋1|＋|x－1|.

【题目】阅读理解

阅读下列短文，从每题所给的四个选项（A 、B 、C 和 D ）中，选出最佳选项。

The ancient city of Xi'an in China holds many treasures. And last month, archaeologists working there made an important discovery—a buried palace built in the third century B.C. to honor China's first emperor.

The entire palace measures roughly 2,260 feet long by 820 feet wide. It includes 10 courtyard houses and one main building. Archaeologists found bricks and pieces of pottery at the site of the palace, as well as the remains of walls and roads.

The palace is part of the massive burial complex of Emperor Qin Shihuangdi. He conquered seven warring kingdoms and united ancient China in 211 B.C.

Qin Shihuangdi wanted his legacy, or accomplishments, to be remembered forever. So he hired more than 700,000 workers to build his funeral complex in Xi'an. It represents a miniature version of his vast kingdom.

The complex also includes the world-famous terra-cotta army, a collection of more than 8,000 life-size clay statues. These sculptures represent soldiers, acrobats, and horses from the Qin Dynasty (221 B.C.-206 B.C.). Scientists have not yet found all these terra-cotta warriors, even though they discovered more of the statues last summer.

Farmers discovered the complex by accident in 1974. Since then, scientists studying the site have learned a great deal about life in ancient China. But much of the emperor's tomb has yet to be dug up, or unearthed. Many of the artifacts (objects from the past) are so old that scientists cannot preserve them.

"Archaeologists fully acknowledge that nobody in the world has the technology (to safely dig up Xi'an's treasures) yet," explains Kristin Romey, an expert on Chinese archaeology.

But as technology improves, archaeologists will keep digging to uncover the rest of the wonders that still lie buried in Xi'an.

"It's one of the most important archaeological discoveries that's waiting to be made," says Romey, "and we know where it is."

【1】How long is the history of the newly found palace?

A. About 820 years.

B. About 2,000 years.

C. About 2,200 years.

D. About 2,400 years.

【2】Why did Qin Shihuang have people build his tomb?

A. To keep all of his treasures in store.

B. To expect people to remember him forever.

C. To prevent his body from disappearing soon.

D. To collect more than 8,000 life-size clay soldiers.

【3】What causes trouble to dig out the emperor's tomb?

A. The local government doesn't support it.

B. Archaeologists are in great need.

C. There isn't plenty of money.

D. Technology isn't advanced yet.

【4】What might be the most suitable title for the passage?

A. An Ancient Palace is Uncovered

B. More Terra-cotta Warriors Are Found

C. Archeologists Are Waiting to Dig a Tomb

D. Technology Helps Discover the New Wonder

【题目】【2017年高考浙江卷卷】阅读下面的文字，完成文后各题。

一种美味

巩高峰

他清晰地记得，六岁那年夏天的那个傍晚，当他把一条巴掌大的草鱼捧到母亲面前时，母亲眼里第一次出现了一种陌生的光。他甚至觉得，他在母亲眼里一定是突然有了地位的，这种感觉在随后下地干活回来的父亲和两位哥哥眼里也得到了证实。

他有些受宠若惊。此前，他的生活就是满村子蹿，上树掏鸟窝，扒房檐摘桃偷瓜。因此，每天的饭都没准时过，啥时肚子饿了回家吃饭，都要先挨上父亲或母亲的一顿打才能挨着饭碗的边儿。

那天不一样，母亲把双手在围裙上擦了又擦。母亲终于接过那条鱼时，他忽然有一点点失望，那条本来大得超出他意料的鱼，在母亲的双手之间动弹时，竟然显得那么瘦小。

准确地说，在那之前他没吃过鱼，唇齿间也回荡不起勾涎引馋的味道。他相信两个哥哥应该也极少尝过这东西。在母亲的招呼下，他们手忙脚乱地争抢母亲递过的准备装豆腐的瓷碗。豆腐，是跟年联系在一起的东西了。天！为了那条鱼，母亲要舀一瓷碗的黄豆种子去换半瓷碗的豆腐来搭配。隐隐约约地，他有了美味的概念，还有慢慢浓起来的期待。

父亲坐在灶前一边看着火苗舔着锅底，一边简单地埋怨了几句，似乎是嫌母亲把鱼洗得太干净了，没了鱼腥味。这已经是难得的意外了，平日里，父亲一个礼拜可能也就说这么一句话。父亲埋怨时，母亲正在把那条鱼放进锅里，她轻手轻脚，似乎开了膛破了肚的草鱼还会有被烫痛的感觉。父亲笑了笑，带着点儿嘲意。母亲嗔怪着说，你笑什么笑！鱼真的还没死，还在锅里游呢。说着，母亲还掀了锅盖让父亲看。父亲保持着笑意，不愿起身。

母亲拿着装了葱段蒜末的碗，就那么站着等水烧开。

他则坐在桌前，看这一切时他是不是双手托着腮？他忘了。反正所有的记忆都是那条鱼和围绕着那条鱼而产生的梦一般陌生的气息。那天什么活都不用他干，他是这顿美味的缔造者，可以游手好闲。父母的举动让他觉得他有这个资格。

在豆腐到来时，母亲甚至都没来得及埋怨一下一贯喜欢缺斤短两的豆腐贩子，因为豆腐马上就被切成块下了锅。美味，让他带着很多的迫不及待，还有一点点的张皇。张皇什么呢？鱼都在锅里了，它还能游回村头那条沟里去？不过这种张皇让他有点儿熟悉，在沟里捉到鱼时他也这么心慌来着，因为连他自己都不相信，那条沟里竟然会有鱼。

来不及细细回味了，豆腐一下锅，屋子里顿时鲜香扑鼻。他是第一次知道，鱼的味道原来是这样的，新鲜得让人稍稍发晕。在鱼汤从锅里到上桌之间，他拼命地翕动鼻翼，贪婪地往肺里装这些味道。他相信装得越多，回味的时间就越长。

至于那锅鱼汤具体是什么滋味，他倒完全不记得哪怕一点儿细节。因为全家吃饭喝鱼汤的状态都有些鲁莽，只有嘴唇和汤接触的呼呼声，一碗接一碗时勺子与锅碰撞的叮当声，还有一口与另一口之间换气时隐约的急促。

那天饭桌上的气氛也不一样，一家人习惯的默不作声完全没了踪影，父亲开口谈天气了，两个哥哥则说了今年可能的收成。而母亲，只是嘴含笑意，一遍又一遍地给大家盛汤。

最后，父亲说了一句有点儿没头没脑的话，父亲说，三子该上学了。

他就叫三子。如今回想起来，对鱼汤食不知味的原因应该就是这句话。两个哥哥没进过一天学校的大门。现在到了他三子，父亲说他该上学了。该，就是要，快要的意思。他忘了两个哥哥投过来的眼神的内容，他忘了鱼汤是什么味道，他忘了那个晚上的一切细节。

美味？美味是什么味呢？当他终于能背着书包从村头墙角中出来，忸怩地走进学校的大门，他离美味的书面意思越来越近。但是，他知道美味的真正意思并不是之后的上学，仍然是有鱼的那天晚上——

两个哥哥忽然就饱了，先后离开桌子回屋睡觉，可是鱼汤每个人起码还可以盛两碗。他们没解释为什么，也不用解释，地里的活要起早贪黑，否则这种鱼加豆腐的美味只能还是好多年享受一次。父亲愣了愣，恢复了以往不苟言笑的表情。母亲端着碗，出神，她似乎用眼神示意过父亲别口不择言，但是现在她卸去了笑容，朝着屋外黑糊糊的夜空，一直出神。

可是羊要进圈，牛要喂草，猪还要吃食。都这么愣着不能解决一点儿问题。他起身去做，也只有他还有心情做。

坐在灶前添柴火煮猪食时，已经是最后一件事了。把火点着，添第二把柴火的时候，他就抓着了一个黏黏软软的东西，凑到灶前的火光里一看，是那条鱼！从锅里蹦到地面，它显然已经超越了极限。现在，它早已死了，只是眼里还闪着一丝诡异的光。

（本文有删改）

【1】理解文中加点词语的含义。

（1）陌生的光

（2）陌生的气息

【2】赏析文中画线的句子。

【3】“一种美味”有多重意蕴，试简要分析。

【4】小说设置了一个意外的结尾，这样写有什么好处？

【题目】请你用简洁的说明性文字介绍这幅漫画，不超过35个字，然后用一句话概括它的寓意，不超过25个字。

答：_____________________________________________________________________

_________________________________________________________________________

【题目】短文改错

假定英语课上老师要求同桌之间交换修改作文，请你修改你同桌写的以下作文。文中共有10处语言错误，每句中最多有两处。错误仅涉及一个单词的增加、删除或修改。

增加：在缺词处加一个漏字符号()，并在其下面写出该加的词。

删除：把多余的词用(＼)划掉。

修改：在错的词下划一横线，并在该词下面写出修改后的词。

注意：1. 每处错误及其修改均仅限一词；

2. 只允许修改10处，多者（从第11处起）不计分。

We receive your application last week. We regret to inform you that our company has employed a boy calling Tony for the job. Having studied your information careful, we decided that we should employ someone with more office experiences for this particular position. You have impressed them with your determination to learn and your ability to work hard, but we do hope that you will apply for a position in our company sometime in the future. We would like to thank you on your being interested our company. Please to email us if there is any further questions.

【题目】（五）

请根据你对这幅画的理解用英语写一篇短文。内容要求：

1.描述漫画内容，如情景，人物，动作等。

2.结合自身实际，谈谈你的感想。

3.举例说明你能在尊老爱老方面做些什么。

注意：

1.词数120左右。

2.参考词汇：按摩 massage n.﹠v.

试题分类